Exercícios de Diagrama T × S - Lista de Exercícios Resolvida
Questão 1
Um mol de um gás ideal é submetido a um ciclo reversível consistindo de duas ADIABÁTICAS e duas ISÓCORAS, como mostra o diagrama - na figura.
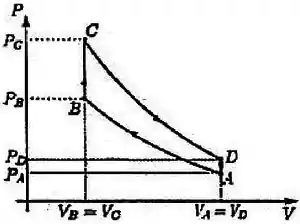
Marque a opção que melhor representa o MESMO ciclo em um diagrama -.
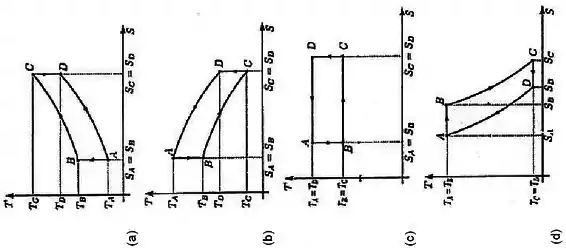
Questão 2
de um gás ideal é submetido a uma transformação cíclica reversível, representada no plano pelo diagrama abaixo:
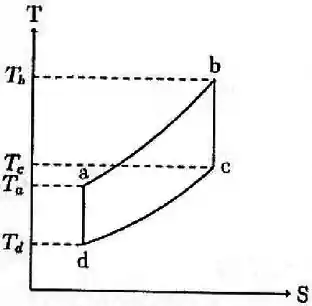
Na transformação , o gás sofre um aquecimento a pressão constante; em , um resfriamento adiabático; em , um resfriamento a volume constante; finalmente, em , um aquecimento adiabático.
Mostre, partindo de primeiros princípios, que
Dado que, no aquecimento a pressão constante, e, no resfriamento a volume constante, , calcule o trabalho realizado neste ciclo.
Desenhe o diagrama correspondente no plano , descrevendo cada processo, e calcule o trabalho, da maneira tradicional,APENAS no processo a pressão constante . Escreva o resultado em termos das temperaturas do sistema.
Ver solução completaQuestão 3
O ciclo de combustão interna de um motor a gasolina dos carros é conhecido como Ciclo Otto. O ciclo opera entre quatro processos, dois isocóricos (volume constante), onde ocorrem as trocas de calor, intercalados por dois adiabáticos, sem trocas de calor. No processo ocorre a queima do combustível na explosão fazendo com que a temperatura varie, e no processo ocorre o escape dos gases produtos da queima, variando a temperatura de . Suponha que os processo sejam quasi-estáticos e que o gás seja ideal.
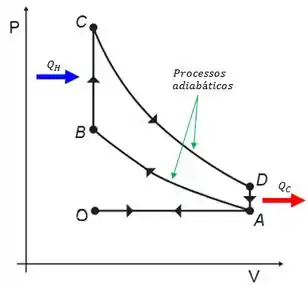
Represente o Ciclo Otto num diagrama .
Ver solução completaQuestão 4
Seja o ciclo abaixo, realizado por n moles de um gás ideal, no plano . Considere conhecidas as temperaturas e e a diferença de entropia .
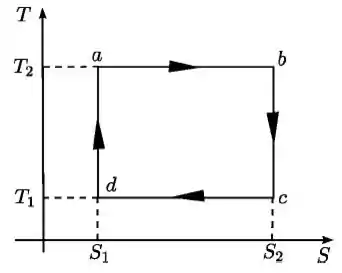
Calcule o trabalho total do ciclo em função de . Este ciclo representa uma máquina ou um refrigerador? Justifique.
Ver solução completaQuestão 5
A figura mostra um processo cíclico, sofrido por moles de um gás ideal monoatômico, representado pelo plano , onde é a energia interna do sistema, e é a entropia. A respeito desse sistema, responda as seguintes questões:
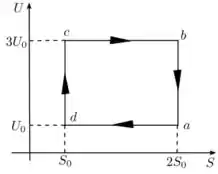
Identifique cada processo, isso é, se é isocórico, isotérmico, isobárico ou adiabático.
Calcule o trabalho realizado pelo sistema e o calor trocado por ele em cada etapa em termos de Indique explicitamente a convenção de sinais adotada.
Diga se o ciclo corresponde a uma máquina térmica ou a um refrigerador. Se for uma máquina, calcule a eficiência térmica, se for um refrigerador, calcule o coeficiente de desempenho.
O que podemos dizer desse ciclo em relação ao ciclo de Carnot? Qual é o mais eficiente?( Ou de melhor desempenho?).
Ver solução completaQuestão 6
A figura mostra um processo cíclico, sofrido por moles de um gás ideal monoatômico, representado pelo plano , onde é a energia interna do sistema, e é a entropia. A respeito desse sistema, responda as seguintes questões:
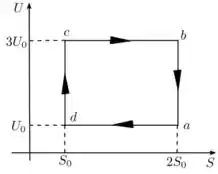
- Identifique cada processo, isso é, se é isocórico, isotérmico, isobárico ou adiabático.
- Calcule o trabalho realizado pelo sistema e o calor trocado por ele em cada etapa em termos de Indique explicitamente a convenção de sinais adotada.
- Diga se o ciclo corresponde a uma máquina térmica ou a um refrigerador. Se for uma máquina, calcule a eficiência térmica, se for um refrigerador, calcule o coeficiente de desempenho.
- O que podemos dizer desse ciclo em relação ao ciclo de Carnot? Qual é o mais eficiente?( Ou de melhor desempenho?).
Questão 7
Três mols de um gás ideal monoatômico passam pelo ciclo termodinâmico descrito na figura( isobárico, isotérmico e isocórico):
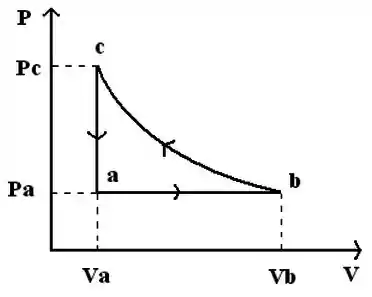
Dados , e , determine , e (tome e trabalhe com dois algarismos significativos).
Determine o trabalho realizado pelo sistema , o calor cedido ao sistema e a variação da energia interna para cada processo e preencha a tabela (justifique cada valor encontrado):

O ciclo considerado descreve uma máquina térmica ou um refrigerador? Justifique
Calcule a eficiência (se for máquina), ou coeficiente de desempenho (se for refrigerador), do ciclo.
Faça um gráfico do ciclo considerado.
Ver solução completaQuestão 8
Um mol de um gás ideal é submetido a um ciclo reversível consistindo de duas ADIABÁTICAS e duas ISÓCORAS, como mostra o diagrama PV na figura.
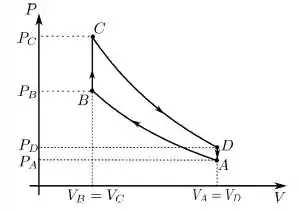
Marque a opção que melhor representa o MESMO ciclo em um diagrama TS.
Escolha uma opção:
a.
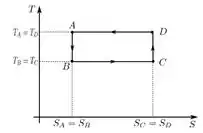
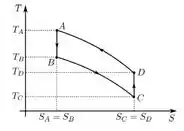
b.
c.

d.
Questão 9
Um bloco que desliza sobre uma superfície áspera desacelera e eventualmente e para. O processo inverso nunca ocorre. Ou seja, um bloco em repouso nunca começa a se mover e acelerar em uma superfície áspera sem a ação de um agente externo. A segunda situação é proibida porque violaria
- conservação da energia total.
- conservação do momento.
- a primeira lei da termodinâmica.
- a segunda lei da termodinâmica.
- tanto a primeira como a segunda leis da termodinâmica.
Questão 10
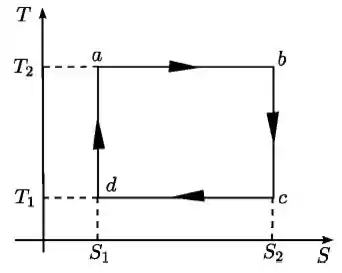
Seja o ciclo abaixo, realizado por n moles de um gás ideal, no plano . Considere conhecidas as temperaturas e e a diferença de entropia
- Calcule o calor transferido em cada etapa ( em função de , , indicando se este foi absorvido pelo sistema ou cedido pelo mesmo.
- Calcule a diferença de energia interna em cada etapa ( em função de , onde é a capacidade térmica molar a volume constante do gás.
- Calcule o trabalho total do ciclo, em função de , indicando claramente se este foi realizado pelo sistema ou sobre ele.
- Este ciclo representa uma máquina ou um refrigerador? Justifique. Se você achar que representa uma máquina, calcule a sua eficiência térmica Se você achar que é um refrigerador, calcule o coeficiente de desempenho
Questão 11
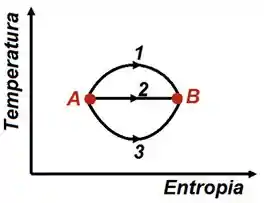
Um sistema termodinâmico pode ir do estado para o estado através de três processos reversíveis distintos, conforme ilustrado no diagrama abaixo. Sendo , e os calores recebidos pelo sistema nos processos , e respectivamente e , e as respectivas variações de energia interna, marque a alternativa correta.
Questão 12
Suponha que () de um gás diatômico ideal () opera em uma máquina de Carnot entre as temperaturas de e . A pressão em é 6. Na expansão isotérmica o volume é duplicado.
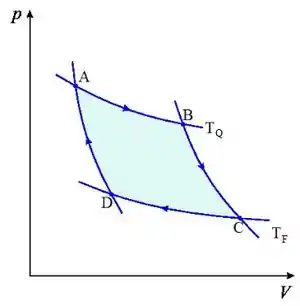
Dados: AB e CD são isotermas, BC e DA são adiabáticas.
a) Calcule a pressão e o volume nos pontos A, B, C e D do diagrama PV da figura.
b) Calcule o calor, o trabalho e a transformação de energia interna para cada transformação do ciclo.
c) Calcule a eficiência da máquina.
d) Calcule a variação de entropia em cada transformação do ciclo e represente o ciclo num diagrama T S (temperatura do gás em função da entropia) identificando os estados térmicos A, B, C e D.
Ver solução completaQuestão 13
Uma máquina térmica usa, como fluido de trabalho, dois moles de um gás ideal diatômico, cuja capacidade térmica molar vale . O gás é submetido aos seguintes processos reversíveis:
Uma compressão adiabática, partindo de uma temperatura e de um volume , até que seu volume se reduza a metade, no estado .
Uma expansão isotérmica, do estado até o estado , onde seu volume retorna ao valor inicial.
( Um resfriamento isocórico, até que sua temperatura volte ao valor inicial, fechando assim o ciclo.
- Determine temperatura do gás no estado .
- Determine o calor transferido ao gás em cada uma das etapas.
- Determine a variação da entropia do gás em cada uma das etapas.
- Dado que o valor da entropia no estado vale , faça um esboço deste ciclo num diagrama , deixando claro cada uma das etapas.
Atenção: Deixe suas respostas em termos de e . Se achar conveniente, use que
Ver solução completaQuestão 14
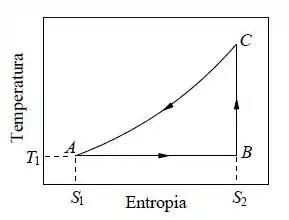
Um gás ideal monoatômico () é submetido a um ciclo termodinâmico composto por três processos reversíveis, um isotérmico, outro adiabático e o terceiro isobárico. O ciclo está esquematizado no diagrama da figura abaixo. Suponha que e e que a base neperiana vale , por simplicidade.
- Determine a variação da energia interna do gás no processo .
- Se o volume do gás é no ponto , quantos litros ele ocupa no ponto ?
Questão 15
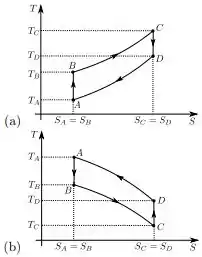
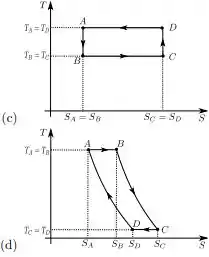
Um mol de um gás ideal é submetido a um ciclo reversível consistindo de duas ADIABÁTICAS e duas ISOCÓRICAS, como mostra o diagrama na figura.
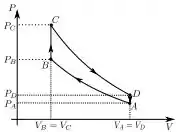
Marque a opção que melhor representa o MESMO ciclo em um diagrama .
Questão 16
O ciclo de combustão interna de um motor a gasolina dos carros é conhecido como ciclo de Otto. O ciclo opera entre quatro processos, dois isocóricos (volume constante), onde ocorrem as trocas de calor, intercalados por dois adiabáticos, sem trocas de calor. No processo ocorre a queima do combustível na explosão fazendo com que a temperatura varie, e no processo ocorre o escape dos gases produtos da queima, variando a temperatura de . Supondo que os processo seja quase estáticos e que o gás seja ideal o ciclo é representado na figura ao lado num diagrama.
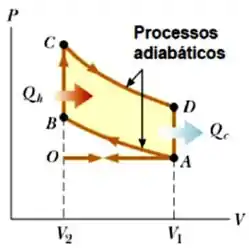
a) Determine o rendimento do ciclo de Otto, em termos de 𝑒
b) Sabendo que um processo adiabático obedece à e considerando escreva a resposta anterior em termos de .
c) Calcule a variação de entropia, , nos processos, e no ciclo completo utilizando a variação de entropia encontrada em cada processo.
d) Represente o ciclo de Otto num diagrama .
Ver solução completaQuestão 17
Um mol de um gás ideal é submetido a um ciclo reversível consistindo de duas ADIABÁTICAS e duas ISÓCORAS, como mostra o diagrama - na figura.
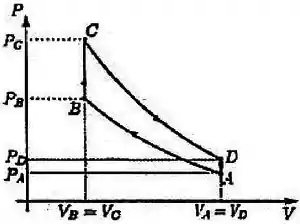
Marque a opção que melhor representa o MESMO ciclo em um diagrama -.
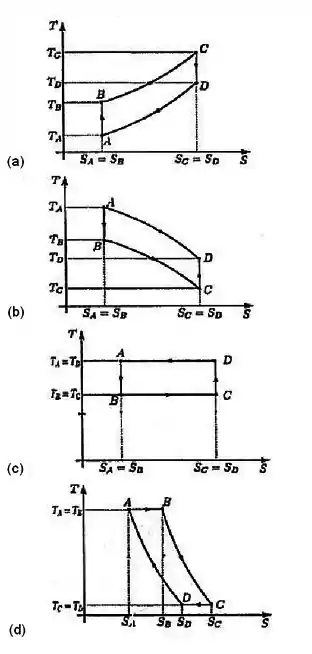
Questão 18
de um gás ideal é submetido a uma transformação cíclica reversível, representada no plano pelo diagrama abaixo:
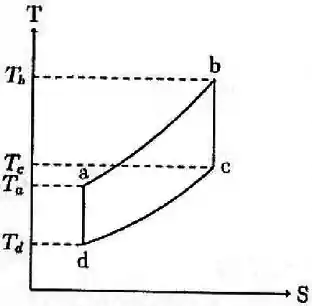
Na transformação , o gás sofre um aquecimento a pressão constante; em , um resfriamento adiabático; em , um resfriamento a volume constante; finalmente, em , um aquecimento adiabático.
- Mostre, partindo de primeiros princípios, que
- Dado que, no aquecimento a pressão constante, e, no resfriamento a volume constante, , calcule o trabalho realizado neste ciclo.
- Desenhe o diagrama correspondente no plano , descrevendo cada processo, e calcule o trabalho, da maneira tradicional,APENAS no processo a pressão constante . Escreva o resultado em termos das temperaturas do sistema.
Questão 19
Considere o ciclo diesel reversível, formado por uma isóbara, uma isócora e duas adiabáticas, realizado por um mol de gás ideal, como representado no diagrama P-V abaixo:
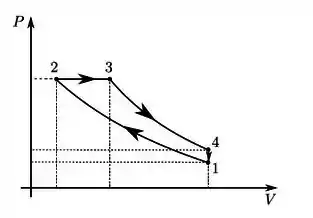
a) Calcule o trabalho total no ciclo, em termos das temperaturas nos estados 1, 2, 3 e 4 e da capacidade térmica molar a volume constante do gás.
b) Calcule o rendimento do ciclo, em termos das temperaturas nos estados 1, 2, 3 e 4 e da razão entre as capacidades térmicas molares à pressão e volume constantes.
c) Represente o ciclo no diagrama S-T, indicando claramente qual o comportamento em cada etapa.
Ver solução completa