Diga se as afirmações abaixo são verdadeiras ou falsas:
- O coeficiente angular (taxa de variação) da função é ;
- O coeficiente Linear da função é ;
- A função é crescente;
- No plano cartesiano, o eixo das ordenadas é equivale ao , enquanto que o eixo das abscissas corresponde ao .
Passo 1
Fala Aíí!! Vamos analisar cada uma das afirmações e verificar quais são verdadeiras e quais são falsas!

Na letra (a) temos a afirmação “O coeficiente angular (taxa de variação) da função é . Vamos lembrar o que é o coeficiente angular de uma função? Em uma função, , o “” é chamado de coeficiente angular ou taxa de variação e está ligado a inclinação da reta em relação ao eixo .
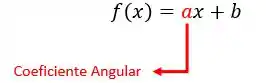
Ou seja, na função o nosso coeficiente angular será o número , e não o como informado na afirmação! Assim, a afirmação é falsa!
Passo 2
b) A letra (b) fala sobre coeficiente linear de uma função. O coeficiente linear de uma função será o termo independente:
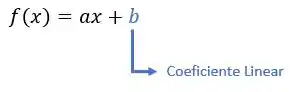
Portanto, na função o coeficiente linear é o termo ! Ou seja, a afirmação é verdadeira!!

Passo 3
c) A afirmação da letra (c) é “A função é crescente”. Uma função será crescente quando
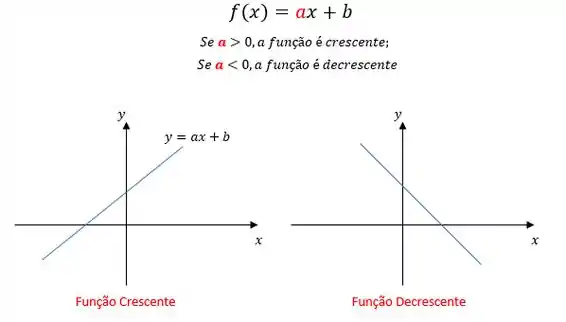
Beleza?! Aqui como o nosso , então a função será decrescente. Ou seja, a afirmação é falsa!!
Passo 4
d) A última afirmação “No plano cartesiano, o eixo das ordenadas é equivale ao , enquanto que o eixo das abscissas corresponde ao fala sobre os eixos do plano cartesiano. Vale lembrar que
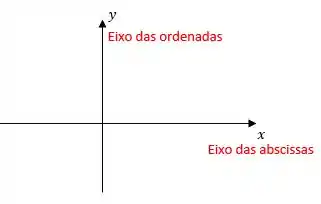
E na afirmação da letra (d) fala exatamente o contrário, rs. Então a afirmação é falsa!
Resposta
- Falsa
- Verdadeira
- Falsa
- Falsa