Resolva o circuito RL:
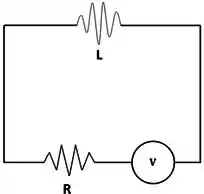
Sabendo que as quedas de voltagem são:
E que a força eletromotriz é:
E com a lei de Kirchoff: ”A soma algébrica de todas as quedas de tensão em torno de qualquer circuito fechado é nula, ou a tensão aplicada em um circuito fechado é igual à soma das quedas de tensão no resto do circuito.”
Passo 1
Eita que doidera, né não?
Mas a gente viu na teoria que por essa lei de Kirchoff podemos concluir que:
Mas sabemos que valor da força eletromotriz é:
Assim:
Passo 2
Beleza clã, achamos uma EDO linear de primeira ordem, né? Vamos dividir tudo por :
Passo 3
Calcular a integral sem adicionar a constante e ache
Assim ficou :
Passo 4
Calcular a integral
Essa integral pode ser resolvida por duas integrações por partes:
Chama de :
Assim:
Mesma coisa:
Perceba que a integral que apareceu na esquerda é igual à da direita, então podemos passar ela para o mesmo lado e colocar ela em evidência:
Assim:
Negócio tá ficando bizarro o.O, mas simbora:
Negócio tá ficando bizarro o.O, mas simbora:
Então:
Vamos tentar dar uma ajeitada pra ficar com uma aparência melhor:
Passo 5
Então qual é a cara da solução?
Bem bem, essa já é a resposta do problema, mas para dar a resposta do gabarito um paranauê precisa ser feito. Se a gente usar essa identidade trigonométrica aqui:
A gente consegue reescrever essa bagaça dessa forma:
Isso é bastante usado no mundo da vibração, mas por aqui ainda é meio assustador, mas é trigonometria!
Subtituindo:
Assim, finalmente:
Uuuuuufaaaaa!!!!