Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Probabilidade Conjunta de V.A. Bidimensionais Discretas

Ver Teoria
Exercício 12345678910111213141516171819

Enunciado

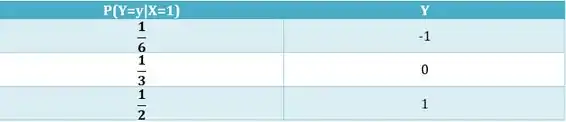
Considere a distribuição conjunta de X e Y, parcialmente conhecida, dada na tabela abaixo.

a) Complete a tabela, considerando X e Y independentes.

b) Obtenha as distribuições condicionais de X, dado que Y=0, e de Y, dado que X=1.

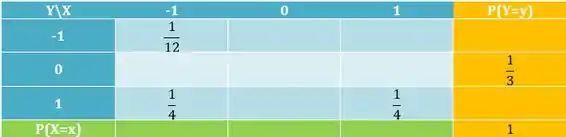
Passo 1

Primero passo é dar nome aos bois hehehe. Ou seja, vamos colocar em cada espaço vazio uma icognita.

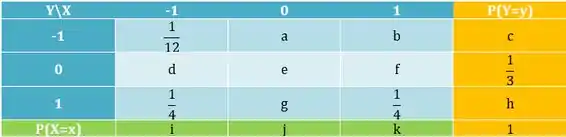
A partir daí é só ir com calma e lembrar que a soma de uma linha/coluna tem que ser igual ao último valor da mesma

  • 2ª coluna:

    • 1 12 + d + 1 4 = i → i = 4 12 + d → i = 1 3 + d  

    Como eles são independentes, sabemos que

    i × 1 3 = d → i 3 = d → i = 3 d

    Substituindo na equação anterior teremos:

    3 d = 1 3 + d → 3 d - d = 1 3 → 2 d = 1 3 → d = 1 6

    Assim

    i = 3 d → i = 3 × 1 6 → i = 1 2

  • 2ª linha com 2ª coluna:

    • Podemos calcular c, pois por serem independentes sabemos que:

    i × c = 1 12 → 1 2 × c = 1 12 → c = 1 6

  • 5ª coluna:

    • Sabemos que a soma da 5ª coluna deve ser igual a 1, portanto

    c + 1 3 + h = 1 → 1 6 + 1 3 + h = 1 → h = 1 - 3 6 → h = 1 2

  • 4ª linha com 4ª coluna:

    • Podemos calcular k por serem independentes. Teremos:

    h × k = 1 4 → 1 2 × k = 1 4 → k = 1 2

  • 5ª linha

    • Sabemos que a soma da última linha deve ser igual a 1, portanto

    i + j + k = 1 → 1 2 + j + 1 2 = 1 → j = 0

  • 3ª coluna

    • Como descobrimos que j = 0 e sabemos que os eventos são independentes, teremos que:

    a = e = g = 0

  • 3ª linha com 4ª coluna

    • Por eles serem independentes podemos afirmar que:

    k × 1 3 = f → 1 2 × 1 3 = f → f = 1 6

  • 2ª linha com 4ª coluna

Por eles serem independentes podemos afirmar que:

k × c = b → 1 2 × 1 6 = b → b = 1 12

Substituindo na tabela teremos:

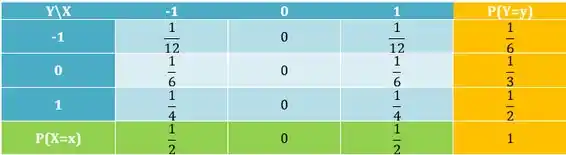
Passo 2

Para calcularmos a condicional precisamos lembrar da formulinha da probabilidade condicional. Vocês lembram?

P A B = P A ∩ B P B

Bom, sabemos na tabela que as probabilidades marginais representam a probabilidade de cada variável aleatória em um certo ponto, enquando os outros componentes das tabelas são das probabilidade conjuntas, da interseção.

Quando pedimos a distribuição condicional de X dado que Y=0 queremos:

P X = - 1 Y = 0

P X = 0 Y = 0

P X = 1 Y = 0

Simbora pras contas então?

  1. P X = - 1 Y = 0

    2. P X = - 1 Y = 0 = P X = - 1 , Y = 0 P Y = 0

    Olhando a tabela sabemos que P X = - 1 , Y = 0 = 1 6 , portanto

    P X = - 1 Y = 0 = P X = - 1 , Y = 0 P Y = 0 = 1 6 1 3 = 1 2

  2. P X = 0 Y = 0

    3. P X = 0 Y = 0 = P X = 0 , Y = 0 P Y = 0

    Olhando a tabela sabemos que P ( X = 0 , Y = 0 ) = 0 , portanto

    P X = 0 Y = 0 = P X = 0 , Y = 0 P Y = 0 = 0

  3. P X = 1 Y = 0

P X = 1 Y = 0 = P X = 1 , Y = 0 P Y = 0

Olhando a tabela sabemos que P X = 1 , Y = 0 = 1 6 , portanto

P X = 1 Y = 0 = P X = 1 , Y = 0 P Y = 0 = 1 6 1 3 = 1 2

Montando uma tabela teríamos:

Passo 3

Faremos o mesmo passo a passo para saber outra probabilidade condicional.

Dessa vez queremos saber a probabilidade condicional de Y dado X = 1 . Queremos:

P Y = - 1 X = 1

P Y = 0 X = 1

P Y = 1 X = 1

Vamos?

  1. P Y = - 1 X = 1

    2. Y = - 1 X = 1 = P X = 1 , Y = - 1 P X = 1

    Olhando na tabela vemos que P X = 1 , Y = - 1 = 1 12 , portanto

    Y = - 1 X = 1 = P X = 1 , Y = - 1 P X = 1 = 1 12 1 2 = 1 6

  2. P Y = 0 X = 1

    3. Olhando na tabela vemos que P X = 1 , Y = 0 = 1 12 , portanto

    Y = - 1 X = 1 = P X = 1 , Y = 0 P X = 1 = 1 6 1 2 = 1 3

  3. P Y = 1 X = 1

Olhando na tabela vemos que P X = 1 , Y = 1 = 1 4 , portanto

Y = - 1 X = 1 = P X = 1 , Y = 1 P X = 1 = 1 4 1 2 = 2

Montando uma tabela:

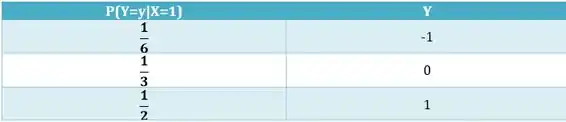
Resposta

a)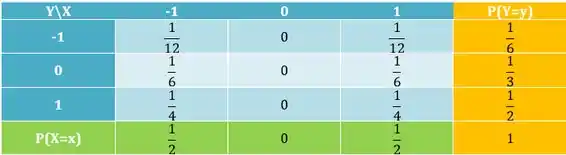

b)

Exercícios de Livros Relacionados

Uma urna contém inicialmente 1 bola vermelha e 1 bola azul. Em cada rodada, uma bola é retirada aleatoriamente e substituída por duas outra bolas de mesma cor (por exemplo, se a bola vermelha ê a prim
Uma pilha do tipo C está em condição de trabalho com probabilidade 0,7 , enquanto uma pilha do tipo D está em condição de trabalho com probabilidade 0,4. Uma piIha é selecionada aleatoriamente de um c
Sorteiam-se bolas de uma urna que contém inicialmente 20 bolas vermelhas e 10 bolas azuis.(a) Qual é a probabilidade de que todas as bolas vermelhas sejam retiradas antes de todas as azuis?Agora supon
No Exemplo 3 f , suponha que a nova evidência esteja sujeita a possíveis interpretaçōes e de fato mostre que é apenas 90 % provável que o criminoso possua a característica em questão. Neste caso, qual
Suponha que 5 % dos homens e 0,25 % das mulheres sejam daltônicos. Uma pessoa daltônica é escolhida aleatoriamente. Qual é a probabilidade dessa pessoa ser um homem? Suponha que exista um mesmo número