Considere um bloco de massa M preso à extremidade de uma mola de constante elástica k e comprimento relaxado e em repouso. A outra extremidade da mola é, então, presa a um dispositivo que oscila com frequência angular e cuja posição é dada por , onde a é uma constante positiva. Suponha que o bloco oscile com a mesma frequência do dispositivo e que o atrito seja desprezível.
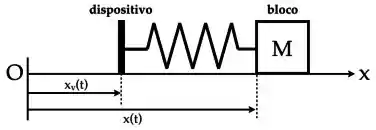
a) Desenhe o diagrama de forças que agem sobre o bloco de massa M e escreva as expressões para os vetores que representam tais forças de forma explícita num sistema de coordenadas apropriado.
(b) Deduza a equação diferencial que descreve o movimento do bloco em termos da variável .
(c) Resolva a equação diferencial encontrando a solução para as condições iniciais do problema.
(d) Qual a frequência do dispositivo para que o sistema entre em ressonância e o que ocorre com a amplitude neste valor de frequência?
Passo 1
a) Temos que desenhar o diagrama de forças. Temos no eixo y, o peso e a normal se compensando. No eixo x, temos uma força restauradora da mola e do sistema de oscilação forçada:
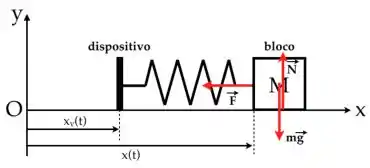
Onde
Já no eixo horizintal, temos a força restauradora da mola
Onde o da mola é o quanto a mola está esticada ou contraída em relação ao dispositivo (). Como o comprimento da mola é , então:
Passo 2
b) Vamos encontrar a equação diferencial desse movimento.
A normal e o peso se anulam, então a única força resultante é a força restauradora.
Então, no eixo x:
Substituindo
Dividindo tudo por m e reorganizando:
O enunciado nos diz para usar a variável . Então,
Então,
Fazendo aquela substituiçãozinha de sempre , chamos na equação:
Passo 3
c) Bora resolver essa EDOzinha aí!
Temos uma equação não homogênea, pois tem um termo que não depende do . Então temos duas soluções, uma homogênea e uma particular
Para calcular a homogênea, basta fingir que não tem nada depois do sinal de igual e resolver normal:
Essa é a famosa EDO do movimento harmônico simples, com solução:
Passo 4
Agora, para a solução particular tem que ser mais criativo. Como a parte não homogênea é oscilatória (), você chuta uma solução também oscilatória e vê no que dá. Por exemplo, vou chutar que a solução particular é:
Jogando isso na EDO inicial:
Como só tem coseno do lado direito, então no lado esquerdo:
O que nos faz chegar em
Juntando tudo:
Passo 5
Podemos juntar as duas soluções agora:
Onde A e são constantes a serem determinadas pelas condições iniciais do problema.
Voltando a variável para , onde
As condições iniciais do problema são (O comprimento relaxado e em repouso):
Aplicando a primeira:
Aplicando a segunda:
Passo 6
Temos que analisar as possibilidades agora,
Dependendo da relação entre e , teremos ou , respeitando que .
Se , então :
Para que isso ocorra, o denominador e o numerador devem ser simultaneamente ambos positivos ou ambos negativos:
e :
Então, , para
Ou então,
e simultaneamente:
Então, , para
No caso de , :
Como , então o numerador e o denomidador devem ter sinais opostos:
Ou e
O que é impossível. Então, para :
e
Logo, para .
Juntando tudo:
Passo 7
d) Para entrar em ressonância, como já sabemos, a frequência externa tem que ser igual a frequência natural de oscilação do sistema.
Mas o que acontece com a amplitude?
Se elevarmos a expressão para a amplitude ao quadrado para não ter que lidar com essas fases diferentes:
Pois , então , chegamos numa expressão única:
Quando
A amplitude diverge, como era esperado, pois não há amortecimento no sistema!
Resposta
a)
b)
c)
Onde e
d) . Amplitude diverge.