Exercícios de Projeto de controlador cascata - Lista de Exercícios Resolvida

Como queria implementar uma malha em cascata para controlar a temperatura de um reator, um engenheiro de controle precisava decidir qual variável intermediária seria mais adequada para usar como variável secudária na malha.

Para isso ele fez o teste de ralé (inserção de um degrau e monitoramento da resposta) na variável primária e nas duas variáveis candidadatas a se tornarem a variável secundária.

Para a variável primária, foi obtida seguinte curva de reação:

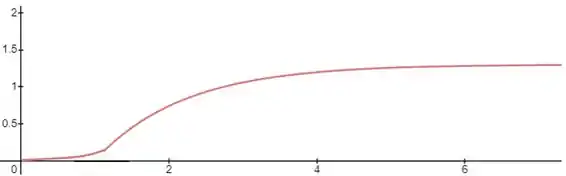
Para a a primeira variável intermediária testada, a curva de resposta é dada abaixo:

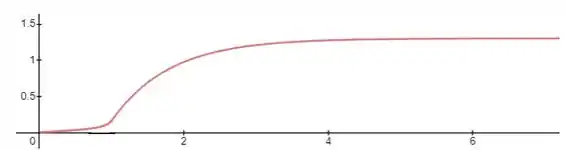
Já para a segunda opção de variável secunária, o gráfico da resposta de reação é dado abaixo:

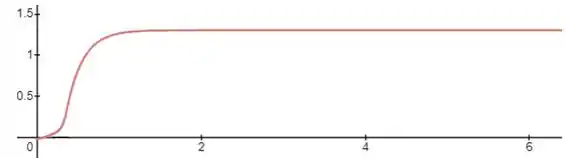
Indique e justifique qual é a melhor opção de escolha para a variável secunária: a primeira ou a segunda opção?

Após a introdução de um degrau unitário no elemento final de controle numa malha em cascata, os comportamentos da variável secundária e as variável primária foram registrados e estão mostrados abaixo respectivamente.

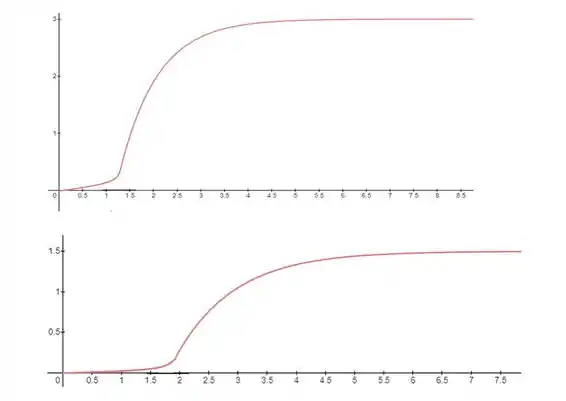
Sintonize ambos os controladores da malha cascata utilizando as correlações de Ziegler-Nichols para a malha secundária e de Austin e Lopez para a malha primária. Suponha um controlador PI secundário e um PID primário

Um engenheiro de controle desejava implementar um sistema de controle cascata em um dos processos pelos quais era responsável visto os vários benefícios agregados pelo controle em cascata em comparação com o controle feedback simples.

Sendo assim, o engenheiro estudou o processo que desejava aplicar o controle em cascata e definiu a variável primária e secundária que seriam usadas.

O próximo passo seria sintonizar os dois controladores, para isso, ele introduziu um degrau unitário no elemento final de controle e registrou a resposta da variável primária e da variável secundária que ele havia escolhido. Com esse registro das respostas ao longo do tempo, ele conseguiu traçar o modelo FOPDT (primeira ordem mais tempo morto) das respostas:

Ao chegar nessa etapa ele notou que não seria possível implementar o controle cascata da forma que ele havia determinado. Explique o motivo e dê uma sugestão do que poderia ser feito.

Após a introdução de um degrau unitário no elemento final de controle numa malha em cascata, os gráficos de curva de reação para a variável primária e secundária foram registrados e estão mostrados abaixo, respectivamente:

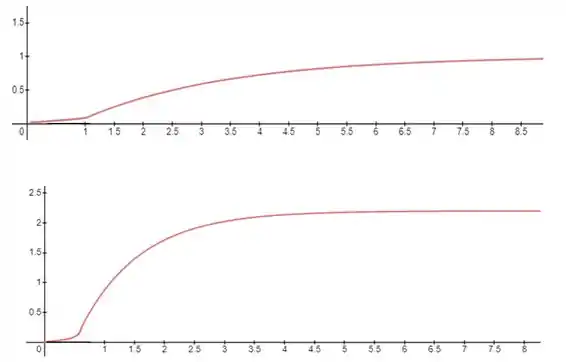
Faça a sintonização dos controladores em casacada. Utilize as correlações de Ziegler-Nichols para o controlador secundário e de Austin e Lopez para o controlador primário. Suponha que o controlador secundário seja do tipo P e o primário é do tipo PI.

Deseja-se sintonizar uma malha em cascata em dois níveis. Para obter os parâmetros de sintonização, introduziu-se um degrau unitário no elemento final de controle e registrou-se as resposta da variável secundária e primária. Após análise das curvas de reação, pode-se deduzir os seguinte modelos FOPDT (primeira ordem mais tempo morto) para as variáveis secundárias e primárias respectivamente:

Sintonize ambos os controladores do sistema em cascata utilizando as correlações de Cohen-Coon para a malha secundária e de Austin e Lopez para a malha primária. Suponha que ambos os controladores sejam do tipo PI.

Após a introdução de um degrau unitário no elemento final de controle numa malha em cascata, os gráficos de curva de reação para a variável primária e secundária foram registrados e estão mostrados abaixo, respectivamente:

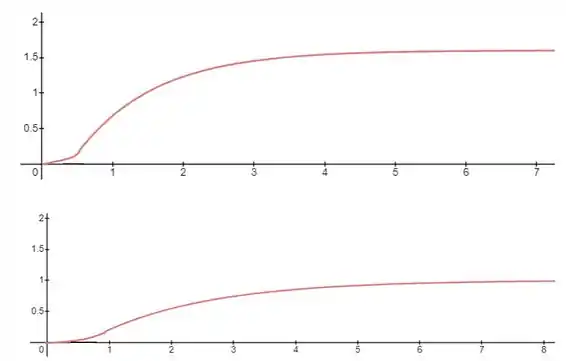
Faça a sintonização dos controladores em casacada. Utilize as correlações de Ziegler-Nichols para o controlador secundário e de Austin e Lopez para o controlador primário. Suponha que o controlador secundário seja do tipo PI e o primário é do tipo PID.

Após a introdução de um degrau unitário no elemento final de controle numa malha em cascata, os comportamentos da variável secundária e as variável primária foram registrados e foi possível aproximar as funções de transferência da malha secundária e primária a um modelo FOPDT como mostrado abaixo:

Sintonize ambos os controladores do sistema, sendo o secundário um controlador P e o primário um controlador PID, utilizando as correlações de Ziegler-Nichols para a malha secundária e de Austin e Lopez para a malha primária.

Após a introdução de um degrau unitário no elemento final de controle numa malha em cascata, os comportamentos da variável secundária e as variável primária foram registrados e foi possível aproximar as funções de transferência da malha secundária e primária a um modelo FOPDT como mostrado abaixo:

Sintonize ambos os controladores do sistema em cascata utilizando as correlações de Ziegler-Nichols para a malha secundária e de Austin e Lopez para a malha primária. Suponha um controlador P secundário e um PI primário