Uma partícula de peso desce de a ao longo da parábola . Agem sobre a partícula a força de gravidade e também uma força horizontal dirigida para a direita, de módulo igual à coordenada do ponto. Determine o trabalho realizado por essas duas forças.
Passo 1
Ele quer o valor do trabalho e sabemos que um trabalho a essa altura do campeonato é nos dado por...
Escrito na forma usual (na forma como vamos trabalhar) vamos ter
O nosso trabalho será basicamente então achar essa força e uma parametrização do caminho. Vamos começar pela força. Venha comigo!
Passo 2
O problema nos disse que a força grandona do qual queremos o trabalho é resultante de outras duas forças:
1º A força horizontal , onde o problema afirma ser para a direita, logo ela é múltipla do vetor e tem módulo igual à coordenada do ponto. Logo...
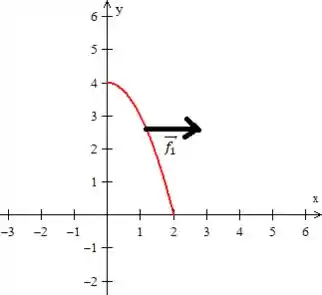
2º A força vertical é o próprio peso, e como ela está apontada para baixo ela é múltipla do vetor ... Seu módulo é igual ao próprio peso :
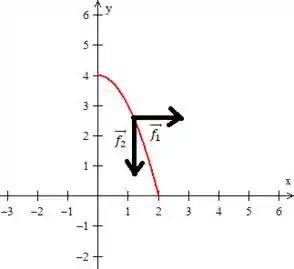
Logo, a força resultante é a soma das duas:
Passo 3
Vamos achar agora a parametrização! Essa é a parábola que a partícula descreve:
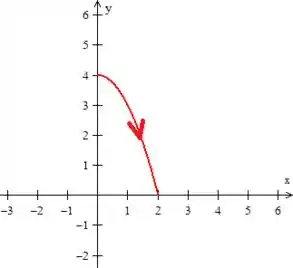
Se chamarmos , o já sai em função do parâmetro , ou seja, podemos realizar uma parametrização explícita
Então
Se ele vai do ponto ao ponto podemos ver que vai de a , que é a coordenada
Passo 4
Precisamos, agora, achar
Passo 5
Retornando para a integral que buscamos a solução
e substituindo os caras que encontramos, não esquecendo de trocar pelos termos do parâmetro ...