Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Centro de Massa e Momento de Inércia

Ver Teoria
Exercício 181234567891011121314151617

Enunciado

20) Mostre que o momento de inércia em relação ao eixo z da casca do cone z = x 2 + y 2 de altura h que está no primeiro octante com densidade constante é I = M h 2 2 , onde M é a massa total.

Passo 1

Se o problema quer momento de inércia em relação ao eixo z ( I z ), o momento em relação ao eixo z vamos dar:

I z = ∬ S   x 2 + y 2 ρ x ,   y ,   z d S

A função de densidade é constante k ...

I z = k ∬ S   x 2 + y 2 d S

Para resolver uma integral de superfície escalar como essa, vamos realizar basicamente três procedimentos centrais:

1º - Parametrizar a superfície S .

2º - Encontrar o termo d S .

3º - Substituir os termos da parametrização na função a ser integrada.

Então, mão a obra ;)

Passo 2

A superfície é, de acordo com o enunciado, esse pedaço de cone:

z = x 2 + y 2

Note que a superfície S já é esse cilindro. Porem não queremos o cone todo neh? É por isso que limitamos somente até uma altura h .

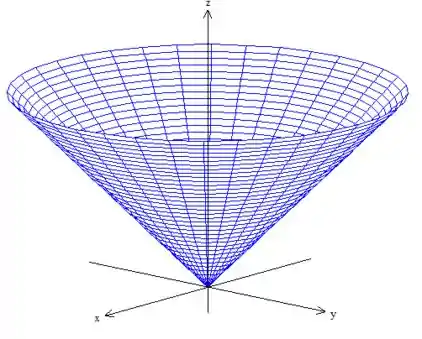
Além disso, estamos no primeiro octante apenas...

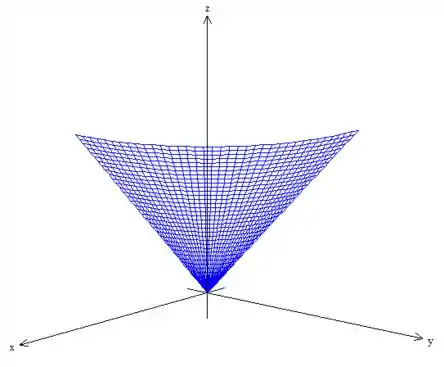
Eis a superfície ;)

Passo 3

Uma superfície cônica podemos sempre parametrizar com as primas das mudanças para coordenadas cilíndricas...

x = r cos ⁡ θ

y = r sin ⁡ θ

Como z é o cone...

z = x 2 + y 2       →

z = r 2 cos 2 ⁡ θ + r 2 sin 2 ⁡ θ   →

z = r 2 cos 2 ⁡ θ + sin 2 ⁡ θ   →

z = r 2 = r

Então a parametrização é...

σ r , θ = r cos ⁡ θ , r sin ⁡ θ ,   r

Passo 4

É importante conhecermos o domínio dos parâmetros... Onde eles variam, saca?

O θ gira até 90 ° para fazer o cone limitado ao primeiro quadrante...

0 ≤ θ ≤ π 2

Já o z , varia até a altura máxima...

0 ≤ z ≤ a l t u r a   h →

0 ≤ z ≤ h       →

Como z = r , então o parâmetro r ...

0 ≤ r ≤ h

Passo 5

Falta-nos encontrar o termo d S ...

d S = N →   d r d θ

Onde...

N → = ∂ σ r , θ ∂ r × ∂ σ r , θ ∂ θ

Calculando as derivadas parciais...

σ r , θ = r cos ⁡ θ , r sin ⁡ θ ,   r                       →                       ∂ σ r , θ ∂ r = cos ⁡ θ , sin ⁡ θ ,   1

σ r , θ = r cos ⁡ θ , r sin ⁡ θ ,   r                       →                 ��     ∂ σ r , θ ∂ θ = - r sin ⁡ θ , r cos ⁡ θ ,   0

N → = i → j → k → cos ⁡ θ sin ⁡ θ 1 - r sin ⁡ θ r cos ⁡ θ 0 =

- r sin ⁡ θ j → + r cos 2 ⁡ θ k → - r cos ⁡ θ i → - r sin 2 ⁡ θ k → =

- r cos ⁡ θ i → - r sin ⁡ θ j → + r cos 2 ⁡ θ + sin 2 ⁡ θ k → =

- r cos ⁡ θ i → - r sin ⁡ θ j → + r k →

Portanto o vetor normal à superfície é...

N → = - r cos ⁡ θ , - r sin ⁡ θ ,   r

Como nos importamos com o módulo de N → , não precisa se importar com o sinal dele...

N → = - r cos ⁡ θ 2 + - r sin ⁡ θ 2 + r 2   →

N → = r 2 cos 2 ⁡ θ + r 2 sin 2 ⁡ θ + r 2 →

N → = r 2 + r 2 = r 2

Então...

d S = r 2   d r d θ

Passo 6

Antes de retornar à integral

I z = k ∬ S   x 2 + y 2 d S

e simplesmente substituirmos tudo, vamos transformar a função escalar que estamos integrando em termos dos parâmetros da superfície...

x 2 + y 2     →         r 2 cos 2 ⁡ θ + r 2 sin 2 ⁡ θ =

r 2

Passo 7

Dado as variações dos parâmetros...

0 ≤ θ ≤ π 2

0 ≤ r ≤ h

E lembrando que...

d S = r 2   d r d θ

e acabamos de ver...

x 2 + y 2 z     →   r 2

A integral de superfície então se transforma em uma...

I z = k ∬ S   x 2 + y 2 d S = k ∫ 0 π 2 ∫ 0 h r 2 ⋅ r 2     d r d θ =

k 2 ∫ 0 π 2 ∫ 0 h r 3     d r d θ

Integral Dupla. ! Bora calcula-la?

Passo 8

Calculando a integral de dentro...

k 2 ∫ 0 π 2 ∫ 0 h r 3     d r d θ = k 2 ∫ 0 π 2 ∫ 0 h r 3   d r d θ =

k 2 ∫ 0 π 2 r 4 4 0 h d θ = k 2 h 4 4 ∫ 0 π 2 d θ =

k 2 h 4 4 π 2 = k 2 h 4 8 π

Passo 9

Bem, esse já é o valor do momento de inércia pedido. Porém, o problema vai um pouco mais além e nos pede em função da massa M da superfície.

A massa de uma superfície é dada também por uma integral de superfície bem especial...

M = ∬ S   ρ x ,   y ,   z d S

Como a função densidade é k ...

M = k ∬ S   d S

Substituindo tudo já encontrado...

M = k ∫ 0 π 2 ∫ 0 h r 2   d r   d θ =

k 2 ∫ 0 π 2 ∫ 0 h r   d r d θ =

k 2 ∫ 0 π 2 r 2 2 0 h d θ = k 2 h 2 2 ∫ 0 π 2 d θ =

k 2 h 2 2 π 2 = k 2 h 2 π 4

Como o momento de inércia é

I z = k 2 h 4 8 π =

k 2 h 2 π 4 h 2 2 =

M h 2 2

Resposta

I z = k ∬ S   x 2 + y 2 d S = k 2 h 4 8 π

E

M = k ∬ S   d S = k 2 h 2 π 4

Portanto

I z = M h 2 2

Exercícios de Livros Relacionados

Dê uma expressão integral para o momento de inércia I z em torno do eixo z de uma folha fina no formato da suerfície S , se a função densidade é ρ .Determine o momento de inércia em torno do eixo z do
Seja S a parte da esfera x 2 + y ² + z ² = 25 ² ² que está acima do plano z = 4 . Se S tiver densidade constante k , encontre ( a ) o centro de massa e ( b ) o momento de inércia em torno do eixo z .
Determine o centro de massa do hemisfério x 2 + y 2 + z 2 = a 2 , z ≥ 0 , se ele tiver densidade constante.
Uma superfície S é representada pela equação vetorial r →u , v= 4 cos ⁡ u ,4 s e nu,4 v 0 ≤ u ≤ 2 π 0 ≤ v ≤ 2 Determinar a equação cartesiana de SDesenhar sobre a superfície S as curvas coordenadas ob
Calcule o momento de inércia da superfície homogênea, de massa M , de equação x 2 + y 2 = R 2( R0 ) , com 0 ≤ z ≤ 1 em torno do eixo O z .