Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Centro de Massa e Momento de Inércia

Ver Teoria
Exercício 912345678101112131415161718

Enunciado

22) Calcule o centro de massa da superfície homogênea, parte da superfície cônica z 2 = x 2 + y 2 , compreendida entre os planos z = 1 e z = 2 .

Passo 1

O centro de massa de uma superfície S pode ser sempre dado por:

C . M = x c ,   y c ,   z c

Onde essas coordenadas podem ser calculadas como sendo:

x c = ∬ S   x ⋅ ρ x ,   y ,   z   d S M a s s a   S                 ,                   y c = ∬ S   y ⋅ ρ x ,   y ,   z d S M a s s a   S                         e               z c = ∬ S   z ⋅ ρ x ,   y ,   z   d S M a s s a   S

A função de densidade é constante k por ser a superfície é homogênea...

x c = k ∬ S   x   d S M a s s a   S                 ,                   y c = k ∬ S   y d S M a s s a   S                         e               z c = k ∬ S   z   d S M a s s a   S

E sabemos que para calcular uma integral de superfície do caso escalar, podemos sempre seguir o método...

1º - Parametrizar a superfície S .

2º - Encontrar o termo d S .

3º - Substituir os termos da parametrização na função a ser integrada.

Então, mãos a obra ;)

Passo 2

Precisamos da superfície S para parametrizar e quem sabe simplificar aquelas integrais, mas quem é essa superfície?

Ora, sabemos que ela é um pedaço do cone...

  z 2 = x 2 + y 2

Mas compreendida entre dois planos, z = 1 e z = 2 ...

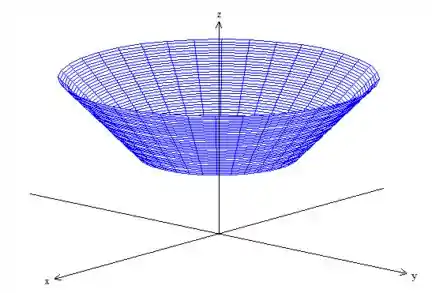
Eis a superfície ;)

Passo 3

Cara! Olha que massa! A superfície S é simétrica em relação à x e a y ! :D

Isso é uma notícia muito boa, pois significa que não precisaremos calcular aquelas integrais para x e a y , pois podemos falar direto que

x c = 0

y c = 0

Legal, neh? Mas tipo, você tem que provar que isso é verdade. Basta você verificar o seguinte:

1º - Provar que a superfície é de fato simétrica em relação a um eixo:

  1. É simétrica em relação ao eixo x , porque não importa se pegar o ponto x ,   y ou - x ,   y , a superfície continua dando os mesmos valores...

    2.   z 2 = - x 2 + y 2 =   z 2 = x 2 + y 2

  2. O mesmo para y ...

  z 2 = x 2 + - y 2 =   z 2 = x 2 + y 2

2º - Bem, quanto a x , a função que estamos calculando a integral é x

∬ S   x   d S

então se pegarmos o ponto f x ,   y ,   z = x = - f - x ,   y ,   z = - - x .

Sacou? é como se tivéssemos somando x de um lado, e do outro na superfície simétrica, - x , por isso que isso dá 0 . O mesmo verifica para y

Passo 4

Agora em relação ao z isso já não acontece, portanto vamos ter que calcular na marra! Portanto parametrizando...

Uma superfície cônica podemos sempre parametrizar com as primas das mudanças para coordenadas cilíndricas...

x = r cos ⁡ θ

y = r sin ⁡ θ

Como z é o cone...

z = x 2 + y 2       →

z = r 2 cos 2 ⁡ θ + r 2 sin 2 ⁡ θ   →

z = r 2 cos 2 ⁡ θ + sin 2 ⁡ θ   →

z = r 2 = r

Então a parametrização é...

σ r , θ = r cos ⁡ θ , r sin ⁡ θ ,   r

Passo 5

É importante conhecermos o domínio dos parâmetros... Onde eles variam, saca?

O θ gira uma volta completa para fazer o cone...

0 ≤ θ ≤ 2 π

Já o z , varia até a altura máxima...

1 ≤ z ≤ 2

Como z = r , então o parâmetro r ...

1 ≤ r ≤ 2

Passo 6

Falta-nos encontrar o termo d S ...

d S = N →   d r d θ

Onde...

N → = ∂ σ r , θ ∂ r × ∂ σ r , θ ∂ θ

Calculando as derivadas parciais...

σ r , θ = r cos ⁡ θ , r sin ⁡ θ ,   r                       →                       ∂ σ r , θ ∂ r = cos ⁡ θ , sin ⁡ θ ,   1

σ r , θ = r cos ⁡ θ , r sin ⁡ θ ,   r                       →                       ∂ σ r , θ ∂ θ = - r sin ⁡ θ , r cos ⁡ θ ,   0

N → = i → j → k → cos ⁡ �� sin ⁡ θ 1 - r sin ⁡ θ r cos ⁡ θ 0 =

- r sin ⁡ θ j → + r cos 2 ⁡ θ k → - r cos ⁡ θ i → - r sin 2 ⁡ θ k → =

- r cos ⁡ θ i → - r sin ⁡ θ j → + r cos 2 ⁡ θ + sin 2 ⁡ θ k → =

- r cos ⁡ θ i → - r sin ⁡ θ j → + r k →

Portanto o vetor normal à superfície é...

N → = - r cos ⁡ θ , - r sin ⁡ θ ,   r

Como nos importamos com o módulo de N → , não precisa se importar com o sinal dele...

N → = - r cos ⁡ θ 2 + - r sin ⁡ θ 2 + r 2   →

N → = r 2 cos 2 ⁡ θ + r 2 sin 2 ⁡ θ + r 2 →

N → = r 2 + r 2 = r 2

Então...

d S = r 2   d r d θ

Passo 7

Antes de retornar à integral

k ∬ S   z   d S

e simplesmente substituirmos tudo, vamos transformar a função escalar que estamos integrando em termos dos parâmetros da superfície...

z     →         r

Passo 8

Dado as variações dos parâmetros...

0 ≤ θ ≤ 2 π

1 ≤ r ≤ 2

E lembrando que...

d S = r 2   d r d θ

e acabamos de ver...

z     →   r

A integral de superfície então se transforma em uma...

k ∬ S   z d S = k ∫ 0 2 π ∫ 1 2 r ⋅ r 2     d r d θ =

k 2 ∫ 0 2 π ∫ 1 2 r 2     d r d θ

Integral Dupla. ! Bora calcula-la?

Passo 9

Calculando a integral de dentro...

k 2 ∫ 0 2 π ∫ 1 2 r 2     d r d θ = k 2 ∫ 0 2 π ∫ 1 2 r 2     d r d θ =

k 2 ∫ 0 2 π r 3 3 1 2 d θ = k 2 2 3 3 - 1 3 ∫ 0 2 π d θ =

k 2 7 3 2 π = k 14 2 π 3

Passo 10

Porém ainda não acabamos! Queremos a coordenada z do centro de massa, lembre-se disso.

z c = k ∬ S   z   d S M a s s a   S =

z c = k 14 2 π 3 M a s s a   S

Falta então encontrar a massa!

A massa de uma superfície é dada também por uma integral de superfície bem especial...

M = ∬ S   ρ x ,   y ,   z d S

Como a função densidade é k ...

M = k ∬ S   d S

Substituindo tudo já encontrado...

M = k ∫ 0 2 π ∫ 1 2 r 2   d r   d θ =

k 2 ∫ 0 2 π ∫ 1 2 r   d r d θ =

k 2 ∫ 0 2 π r 2 2 1 2 d θ = k 2 4 2 - 1 2 ∫ 0 2 π d θ =

3 2 k 2   ⋅ 2 π = 3 k 2 π

Então...

z c = k 14 2 π 3 M a s s a   S = k 14 2 π 3 3 k 2 π =

14 9

Passo 11

O centro de massa, portanto, é...

C . M = x c ,   y c ,   z c =

0 ,   0 , 14 9

Resposta

0 ,   0 , 14 9

Exercícios de Livros Relacionados

Dê uma expressão integral para o momento de inércia I z em torno do eixo z de uma folha fina no formato da suerfície S , se a função densidade é ρ .Determine o momento de inércia em torno do eixo z do
Seja S a parte da esfera x 2 + y ² + z ² = 25 ² ² que está acima do plano z = 4 . Se S tiver densidade constante k , encontre ( a ) o centro de massa e ( b ) o momento de inércia em torno do eixo z .
Determine o centro de massa do hemisfério x 2 + y 2 + z 2 = a 2 , z ≥ 0 , se ele tiver densidade constante.
Uma superfície S é representada pela equação vetorial r →u , v= 4 cos ⁡ u ,4 s e nu,4 v 0 ≤ u ≤ 2 π 0 ≤ v ≤ 2 Determinar a equação cartesiana de SDesenhar sobre a superfície S as curvas coordenadas ob
Calcule o momento de inércia da superfície homogênea, de massa M , de equação x 2 + y 2 = R 2( R0 ) , com 0 ≤ z ≤ 1 em torno do eixo O z .