Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Centro de Massa e Momento de Inércia

Ver Teoria
Exercício 812345679101112131415161718

Enunciado

Integrais de superfície – caso escalar

Calcule a massa de S com densidade superficial de massa δ , onde S é o hemisfério da esfera x 2 + y 2 + z 2 = 6 z tal que z ≤ 3 e δ x , y , z = x 2 + y 2 z .

Passo 1

Para acharmos a massa, temos que fazer a integral de superfície da densidade, ou seja, vai ser uma parada assim

M = ∬ S δ x , y , z d S

Como temos que calcular uma integral de superfície, então, precisamos encontrar uma parametrização para S . Temos a superfície

x 2 + y 2 + z 2 = 6 z

x 2 + y 2 + z - 3 2 = 9

Limitada por z ≤ 3 . Ou seja, temos uma esfera de raio 3 deslocada da origem (centrada em ( 0,0 , 3 ) ) cortada pelo plano z = 3 . Portanto, um casco de esfera:

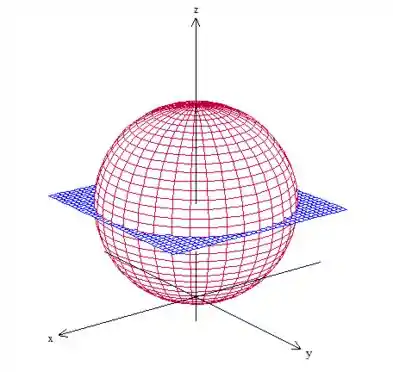
S é a parte da esfera que está abaixo do plano.

Passo 2

Bom, como se trata de uma esfera, vamos usar coordenadas esféricas com ρ = 3 (deslocadas, no caso):

x = 3   s e n   φ   c o s   θ

y = 3 s e n   φ   s e n   θ

z = 3 cos ⁡ φ + 3

Isso nos dá a parametrização

σ θ , φ = 3   s e n   φ   c o s   θ , s e n   φ   s e n   θ , cos ⁡ φ + 1

Bom, como temos uma volta completa em torno do eixo z , 0 ≤ θ ≤ 2 π .

Agora falta o angulo φ .

Com vemos pela figura, ele vai desde onde o plano corta a esfera até π (lembre-se de que, com as coordenadas polares deslocadas, o centro dos eixos coordenados é o centro da esfera!). Fazendo a interseção da esfera com o plano:

z = 3 cos ⁡ φ + 3 = 3

cos ⁡ φ = 0

φ = π 2

Logo, π / 2 ≤ φ ≤ π .

Show?

Passo 3

Agora vamos achar o vetor normal a S :

N r , θ = ∂ σ ∂ φ × ∂ σ ∂ θ

Vamos começar achando as derivadas da parametrização

∂ σ ∂ φ = 3 cos ⁡ φ cos ⁡ θ , cos ⁡ φ s e n   θ , - s e n   φ

∂ σ ∂ θ = 3 - s e n   φ   s e n   θ , s e n   φ cos ⁡ θ , 0

O vetor normal vai ser

N φ , θ = 9 i j k cos ⁡ φ cos ⁡ θ cos ⁡ φ s e n   θ - s e n   φ - s e n   φ   s e n   θ s e n   φ cos ⁡ θ 0

N φ , θ = 9 s e n 2 φ cos ⁡ θ , s e n 2 φ   s e n   θ , cos 2 ⁡ θ s e n   φ cos ⁡ φ + s e n 2 θ   s e n   φ cos ⁡ φ

N φ , θ = 9 s e n 2 φ cos ⁡ θ , s e n 2 φ   s e n   θ , s e n   φ cos ⁡ φ

Passo 4

A norma vai ficar

N φ , θ = 9 s e n 2 φ cos ⁡ θ 2 + s e n 2 φ   s e n   θ 2 + s e n   φ cos ⁡ φ 2

N φ , θ = 9 s e n 2 φ   s e n 2 φ + s e n 2 φ cos 2 ⁡ φ

N φ , θ = 9 s e n φ  

Passo 5

A integral vai ficar

M = ∬ S δ x , y , z d S = ∬ D δ σ φ , θ N φ , θ d φ d θ

Onde D = 0 ≤ θ ≤ 2 π ,   π / 2 ≤ φ ≤ π , como já vimos na parametrização da superfície. Lembrando que

δ x , y , z = x 2 + y 2 z

E que, pela nossa parametrização,

x = 3   s e n   φ   c o s   θ

y = 3 s e n   φ   s e n   θ

z = 3 cos ⁡ φ + 3

Vamos ter

M = ∫ 0 2 π ∫ π / 2 π 9   s e n 2 φ cos 2 ⁡ θ + 9 s e n 2 φ   s e n 2 θ 3 cos ⁡ φ + 3   9 s e n   φ   d φ d θ

= ∫ 0 2 π ∫ π / 2 π 9   s e n 2 φ 3 cos ⁡ φ + 3   9 s e n   φ   d φ d θ =

= 243 ∫ 0 2 π ∫ π / 2 π cos ⁡ φ + 1   s e n 3 φ   d φ d θ =

= 243 ∫ 0 2 π ∫ π / 2 π cos ⁡ φ s e n 3 φ + s e n 3 φ   d φ d θ =

Passo 6

Isso nos dá:

= 486 π ∫ π / 2 π cos ⁡ φ s e n 3 φ + s e n 3 φ   d φ =

= 486 π 1 4 s e n 4 φ π / 2 π + ∫ π / 2 π s e n 3 φ   d φ =

= 486 π 1 4 0 - 1 + ∫ π / 2 π s e n 3 φ   d φ =

= 486 π ∫ π / 2 π s e n 3 φ   d φ - 1 4 =

Agora, nós fazemos o seguinte:

= 486 π ∫ π / 2 π s e n 2 φ   s e n   φ   d φ - 1 4 =

= 486 π ∫ π / 2 π 1 - cos 2 ⁡ φ   s e n   φ   d φ - 1 4 =

= 486 π ∫ π / 2 π s e n   φ - cos 2 ⁡ φ s e n   φ   d φ - 1 4 =

= 486 π - cos ⁡ φ + 1 3 cos 3 ⁡ φ π / 2 π - 1 4 =

= 486 π - - 1 + 1 3 ( - 1 ) - 1 4 =

= 405 π 2

Resposta

405 π 2

Exercícios de Livros Relacionados

Dê uma expressão integral para o momento de inércia I z em torno do eixo z de uma folha fina no formato da suerfície S , se a função densidade é ρ .Determine o momento de inércia em torno do eixo z do
Seja S a parte da esfera x 2 + y ² + z ² = 25 ² ² que está acima do plano z = 4 . Se S tiver densidade constante k , encontre ( a ) o centro de massa e ( b ) o momento de inércia em torno do eixo z .
Determine o centro de massa do hemisfério x 2 + y 2 + z 2 = a 2 , z ≥ 0 , se ele tiver densidade constante.
Uma superfície S é representada pela equação vetorial r →u , v= 4 cos ⁡ u ,4 s e nu,4 v 0 ≤ u ≤ 2 π 0 ≤ v ≤ 2 Determinar a equação cartesiana de SDesenhar sobre a superfície S as curvas coordenadas ob
Calcule o momento de inércia da superfície homogênea, de massa M , de equação x 2 + y 2 = R 2( R0 ) , com 0 ≤ z ≤ 1 em torno do eixo O z .