Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Centro de Massa e Momento de Inércia

Ver Teoria
Exercício 141234567891011121315161718

Enunciado

Integrais de superfície – caso escalar

Calcule a massa da superfície z = x y , satisfazendo x 2 + y 2 ≤ 4 com densidade δ x , y , z = 1 + x 2 + y 2 .

Passo 1

Para acharmos a massa, temos que fazer a integral de superfície da densidade, ou seja, vai ser uma parada assim

M = ∬ S δ x , y , z d S

Vamos, antes de tudo, desenhar essa superfície para termos uma ideia melhor do problema. Temos um cilindro de raio 2 centrado na origem, que corta a superfície z = x y . Mas que superfície é essa? Você não precisa disso para resolver a questão, mas só para você poder visualizar, é uma cela “girada” no plano x y (ou seja, que não tem simetria nos eixos x e y , mas em eixos oblíquos a eles):

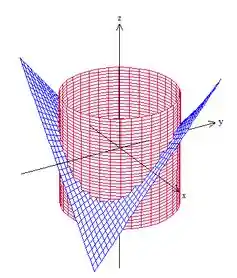
Como o problema pede a parte da superfície que estã dentro do cilindro, queremos isso aqui:

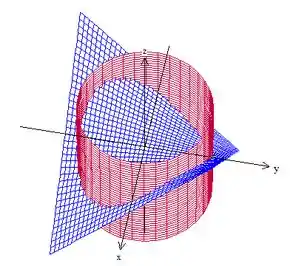
Passo 2

Agora precisamos parametrizar a superfície. Como nossa equação é z = x y , vamos usar x e y como parâmetros, ok? Temos então:

φ x ,   y = ( x , y , x y )

Onde

x 2 + y 2 ≤ 4

Essa é a projeção da nossa superfíce no plano x y , um círculo, pois a superfície azul é cortada pelo cilindro, lembra? Então, vista de cima, ela é um círculo.

Passo 3

Calcular ∂ φ ∂ x e ∂ φ ∂ y

∂ φ ∂ x = ( 1,0 , y )

∂ φ ∂ y = ( 0,1 , x )

Passo 4

Calcular N → x ,   y

N → x , y = ∂ φ ∂ x × ∂ φ ∂ y

N → x , y = 1,0 , y × 0,1 , x

N → x , y = i j k 1 0 y 0 1 x

N → x , y = ( - y ,   - x , 1 )

N → x , y = x 2 + y 2 + 1

Passo 5

A integral vai ficar

M = ∬ S δ x , y , z d S = ∬ D δ σ x , y N x , y d x d y

Onde D =   x 2 + y 2 ≤ 4   , como já vimos na parametrização da superfície. Lembrando que

δ x , y , z = 1 + x 2 + y 2

Vamos ter

M = ∬ D   ( 1 + x 2 + y 2 ) x 2 + y 2 + 1 d x d y

Passo 6

Agora isso aí virou questão de integral dupla, né? Precisamos escrever matematicamente essa região para levar os intervalos para integral.

Olha quantos quadrados nós temos. Nossa região de integração ainda é um círculo. Já sacou que temos que usar oordenadas polares, né? Temos então:

x = r cos ⁡ θ

y = r   s e n   θ

J = r

A região de integração passa a ser então 0 ≤ r ≤ 2 e 0 ≤ θ ≤ 2 π . Substituindo na integral, temos:

= ∫ 0 2 ∫ 0 2 π r r cos ⁡ θ 2 + r   s e n   θ 2 + 1 ( r cos ⁡ θ 2 + r   s e n   θ 2 + 1 )   d θ d r =

= ∫ 0 2 ∫ 0 2 π r ( r 2 + 1 ) r 2 + 1   d θ d r =

Passo 7

Agora vamos resolver a integral. Integrando em relação a θ :

= ∫ 0 2 θ r ( r 2 + 1 ) r 2 + 1 0 2 π   d r =

= 2 π ∫ 0 2 r ( r 2 + 1 ) r 2 + 1   d r =

Agora, para resolver essa integral, podemos fazer a substituição:

r 2 + 1 = u

2 r   d r = d u

Em resumo, chama tudo o que está dentro da raiz de u . Temos então

r = 2         →         u = 5

r = 0         →         u = 1

Levando isso para a integral, temos:

= π ∫ 1 5 u u   d u =

= π ∫ 1 5 u 3 / 2   d u =

Agora podemos integrar:

= 2 π 5   u 5 / 2 1 5 =

= 2 π 5 25 5 - 1 =

Resposta

2 π 5 25 5 - 1

Exercícios de Livros Relacionados

Dê uma expressão integral para o momento de inércia I z em torno do eixo z de uma folha fina no formato da suerfície S , se a função densidade é ρ .Determine o momento de inércia em torno do eixo z do
Seja S a parte da esfera x 2 + y ² + z ² = 25 ² ² que está acima do plano z = 4 . Se S tiver densidade constante k , encontre ( a ) o centro de massa e ( b ) o momento de inércia em torno do eixo z .
Determine o centro de massa do hemisfério x 2 + y 2 + z 2 = a 2 , z ≥ 0 , se ele tiver densidade constante.
Uma superfície S é representada pela equação vetorial r →u , v= 4 cos ⁡ u ,4 s e nu,4 v 0 ≤ u ≤ 2 π 0 ≤ v ≤ 2 Determinar a equação cartesiana de SDesenhar sobre a superfície S as curvas coordenadas ob
Calcule o momento de inércia da superfície homogênea, de massa M , de equação x 2 + y 2 = R 2( R0 ) , com 0 ≤ z ≤ 1 em torno do eixo O z .