Enunciado
21) Calcule o momento de inércia da superfície esférica de raio , homogênea, de massa , em torno de qualquer diâmetro.
Passo 1
Antes de partira para os cálculos, vamos construir o problema. Queremos calcular o momento de inércia de uma esfera de raio qualquer ( é conhecido, portanto ele é uma constante). Esse momento de inércia deve ser calculado em torno de um diâmetro qualquer.
A esfera, vamos desenha-la com o centro na origem do espaço coordenado:
Se o diâmetro pode ser qualquer, vamos pegar o eixo , então queremos o momento de inércia em relação ao (). Pela teoria, calculamos esse momento fazendo...
A função de densidade é constante por ser a superfície é homogênea...
Então bora resolver essa integral!
Passo 2
Para resolver uma integral de superfície escalar como essa, vamos realizar basicamente três procedimentos centrais:
1º - Parametrizar a superfície .
2º - Encontrar o termo .
3º - Substituir os termos da parametrização na função a ser integrada.
Passo 3
Já sabemos quem é a superfície que queremos o momento de inércia:
Esferas podem ser parametrizadas com as primas das coordenadas esféricas...
A diferença é que agora o é o raio da esfera que é fixo – não muda. Ou seja, ...
Lembre-se de que é o raio da semiesfera que o problema pediu para considerar. Ele é um número e não um parâmetro. Sabendo disso a parametrização da esfera ficou então...
Passo 4
É importante conhecermos o domínio dos parâmetros... Onde eles variam, saca?
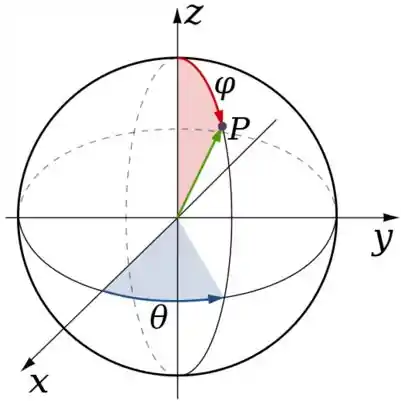
O gira uma volta completa para fazer a esfera...
Já o , varia entre...
Passo 5
Falta-nos encontrar o termo ... Bem, poderíamos encontra fazendo o modelo clássico:
Onde...
Mas cara, não disse que a parametrização é prima das coordenadas esféricas? Então, ela se parece até nisso com ela. Ora quem é o Jacobiano lá?
Então, o módulo do vetor normal será quase isso, basta trocar o pelo raio da esfera...
Então...
Passo 6
Antes de retornar à integral
e simplesmente substituirmos tudo, vamos transformar a função escalar que estamos integrando em termos dos parâmetros da superfície...
Como sabemos...
Então...
Passo 7
Dado as variações dos parâmetros...
E lembrando que...
e acabamos de ver...
A integral de superfície então se transforma em uma...
Como é constante...
Integral Dupla. ! Bora calcula-la?
Passo 8
Fazendo uma substituição...
Mas não se esquecendo de trocar também os limites...
Passo 9
Bem, esse já é o valor do momento de inércia pedido. Porém, o problema vai um pouco mais além e nos pede em função da massa da superfície.
A massa de uma superfície é dada também por uma integral de superfície bem especial...
Como a função densidade é ...
Epa! A integral de é a área da superfície. Como a nossa é uma esfera...
Como o momento de inércia é