Na Figura abaixo, um dipolo elétrico está centralizado na origem, com o vetor momento de dipolo elétrico apontando para o eixo . Deduza uma expressão para o campo elétrico ao longo do eixo , considerando muito maior do que .
Use a série binomial , para o caso .
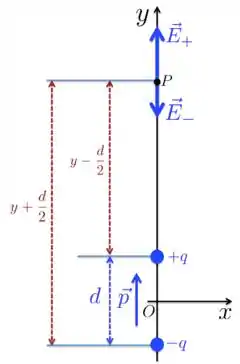
Passo 1
Neste exercício, a gente precisa calcular o campo elétrico resultante , no ponto da Figura acima, produzido pelo par de cargas pontuais fixas e e depois tomar o limite para o obter o valor desse campo resultante quando tem uma distância . Blz? Vamos lá?
Bom, o módulo do campo elétrico produzido pela carga positiva em é:
e pela carga negativa é
O campo elétrico resultante vai estar na direção do eixo e tem módulo dado por
Tranquilo? O módulo do campo resultante é a diferença entre os módulos: .
Passo 2
Agora, para a gente obter o valor desse módulo para , vamos escrever os termos em que aparece na última expressão do passo anterior da seguinte forma
Tranquilo?? Só isolamos o e colocamos para fora dos parênteses, OK?
Para usar a expressão da expansão binomial que foi dada, a gente pode fazer e lá na naquela expressão do binômio. Com isso, teremos que
que, reorganizado, fica assim
Para o outro termo do campo elétrico resultante , teremos, de maneira similar ( e !!), o seguinte
Nesse tipo de expansão, a minha sugestão é que você reconheça na expressão que você quer expandir quem é e quem é . Depois de fazer isso, vai lá para expressão da binomial e substitui esses termos lá, OK?? Daí não vai ter erro...vai por mim...;-)
Bom, mas ainda não acabou o problema...
Passo 3
Agora precisamos substituir essas duas últimas expansões lá na expressão do campo resultante. Mas, olha só, a gente tem termos do tipo nessas expressões, correto?
Como
Isso significa que a gente pode desprezar termos dessa ordem na expansões que acabamos de fazer, blz?
Fazendo isso e já substituindo no módulo do campo elétrico resultante , vamos ter que
Como o vetor momento de dipolo elétrico é dado por , então , temos
Agora, dá uma olhada para essa expressão. Diferente do caso do campo elétrico gerado por uma única carga pontual, depende do inverso da distância ao cubo: !!! Esse é um comportamento geral do campo elétrico produzido por um dipolo elétrico em pontos a distâncias muito grandes comparadas com a distância entre as cargas e . Fechou??
IMPORTANTE: Exercícios com expansões como essa que a gente fez aqui são muito comuns, OK? Então, tente reconhecer quais termos da sua expressão são e e, depois disso, jogue esses valores lá na expansão binomial para não ter erro, valeu…??