Exercícios de Produto Vetorial - Lista de Exercícios Resolvida

Por meio de desenhos simples dos produtos vetoriais aproximados, demonstre que pode ser interpretado como o produto do módulo de vezes o componente de perpendicular a ou o módulo de vezes a componente de perpendicular a

Quais das seguintes operações são legítimas:

Forneça a razão da resposta em cada caso.

1. Prove que dois vetores são anticomutativos para o produto vetorial, ou seja, prove que
2. Se é necessariamente verdadeiro que Explique.

Se são vetores diferentes de zero, é possível que e sejam ambos zero? Explique.

A figura abaixo mostra um paralelogramo cujos lados são os vetores e

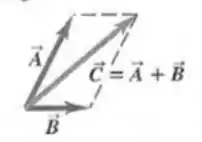
1. Mostre que o módulo do produto vetorial destes vetores é igual à área do paralelogramo . (Sugestão: )
2. Qual é o ângulo entre o produto vetorial e o plano deste paralelogramo?

Dois vetores e possuem módulo de e de . Seu produto vetorial é Qual é o ângulo entre e ?

Para os vetores e indicados na figura abaixo:

1. Ache o módulo e a direção do produto vetorial
2. Ache o módulo e a direção do produto vetorial

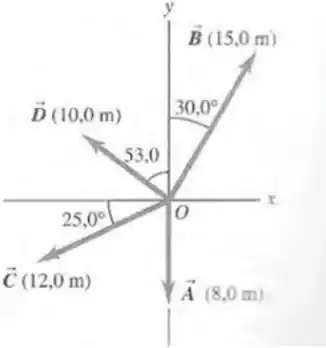
Dados:

Demonstre que, não importa o que sejam, e , .

(Sugestão: não procure uma prova matemática elaborada. Em vez disso, examine a definição da direção do cross product).

Considere os dois produtos vetoriais repetidos e . Forneça um exemplo para mostrar que estes dois vetores normalmente não possuem nem módulo nem direções iguais. Você pode escolher os três vetores de modo que esses dois produtos vetoriais sejam iguais? Em caso afirmativo, forneça um exemplo.

Qual das seguintes operações entre os vetores , e não faz sentido?

(a)

(b)

(c)

(d)

(e)

Dados dois vetores quaisquer e , dependentes do tempo,

1. Mostre explicitamente que

(b) No caso de uma partícula de massa m, se é seu vetor posição e o seu vetor momento linear, mostre que

Considere as seguintes afirmações:

I. O produto vetorial de dois vetores unitários não é um vetor unitário.

II. Para quaisquer dois vetores e e v, u x v != v x u.

III. Para quaisquer três vetores u, v e w (u x v) = u (v x w).

Escolha uma:

a. As afirmativas I e II são verdadeiras.

b. As afirmativas II e III são verdadeiras. X c. Todas as afirmativas são falsas.

d. Todas as afirmativas são verdadeiras.

e. Apenas a afirmativa I é verdadeira.

f. Apenas a afirmativa III é verdadeira.

g. Apenas a afirmativa Il é verdadeira.

h. As afirmativas I e lll são verdadeiras.

Calcule o produto vetorial e entre os vetores mostrados nas figuras.

As coordenadas dos três vértices de um triângulo são (2,1,5), (5,2,8) e (4,8,2). Calcule a área usando o método vetorial