Exercícios de Radiação do Corpo Negro - Lista de Exercícios Resolvida

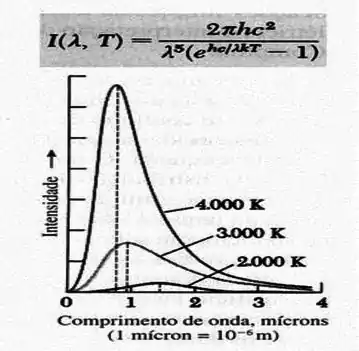
Observe as curvas de Planck da radiação de corpo negro na figura abaixo. Compare-as. Se a temperatura de emissão da radiação aumenta, diga o que ocorre com o comprimento de onda emitido quando a intensidade é máxima.

Considere o uso da lei de Wien () válido aproximadamente para a pele humana. Admita a temperatura da pele .

Determine o comprimento de onda dessa radiação. Diga se está na faixa do visível (

Uma estrela esférica de raio R em equilíbrio térmico à temperatura T emite radiação térmica.

(a) Supondo que a estrela emita energia térmica como um corpo negro, calcule a quantidade de massa ∆m perdida pela estrela durante um intervalo de tempo ∆t.

(b) Um laboratório na Terra observa que o comprimento de onda do máximo da distribuição de radiação térmica da estrela é . Supondo que a estrela esteja se afastando da Terra com velocidade v = 0, 6c, calcule sua temperatura.

Considere o uso da lei de Wien () válido aproximadamente para a pele humana. Admita a temperatura da pele .

Determine o comprimento de onda dessa radiação. Diga se está na faixa do visível (

Considere o uso da lei de Wien () válido aproximadamente para a superfície do asfalto de uma estrada. Admita a temperatura da superfície .

Determine o comprimento de onda dessa radiação. Diga se está na faixa do visível ( a .

De acordo com a hipótese de Planck para a radiação do corpo negro, a energia média de um oscilador é dada pela expressão , onde , para

Determine o valor dessa energia média em termos de para um oscilador que oscile no estado fundamental () com um frequência .

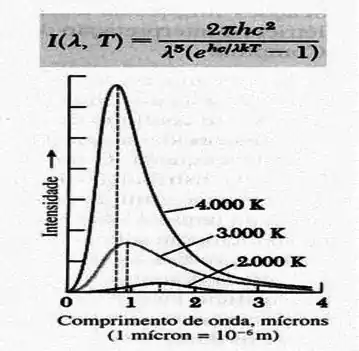
Observe as curvas de Planck da radiaçãoo de corpo negro na figura abaixo. Compare-as. Se a temperatura de emissãoo de radiação aumenta, diga o que ocorre com o comprimento de onda emitido quando a intensidade é máxima.

Considere um planeta que absorve de seu Sol uma potência luminosa total de . É sabido que a área da superfície do planeta é de .

Se nenhum calor é gerado no interior do planeta, para manter a temperatura em equilíbrio o planeta deve emitir de volta para o espaço a mesma quantidade de energia absorvida da luz estelar.

Suponha que o planeta emite radiação como se fosse um corpo negro. Nessas condições, qual é o comprimento de onda para o qual ocorre a máxima intensidade da radiação emitida pelo planeta.

Uma estrela de raio irradia a uma temperatura absoluta . Tratando a estrela como um corpo negro, determine a fórmula para a massa perdida pela estrela num intervalo de tempo .

A emitância espectral de uma estrela atinge o máximo num comprimento de onda igual a .

(a) Calcule a temperatura da estrela.

(b) Se ela tem raio , calcule a potência total emitida pela estrela. Suponha que a estrela emite radiação como um corpo negro.

Uma estrela tem massa , raio e temperatura .

1. Calcule a potência térmica irradiada por esta estrela.
2. Calcule a massa que esta estrela perde por unidade de tempo devido à energia térmica irradiada.
3. Calcule o tempo para que a massa desta estrela diminua de .

Faça a escolha correta e justifique: Para explicar a curva de intensidade da radiação emitida da cavidade, à temperatura T, em função do comprimento de onda, Planck supôs que:

(a) a intensidade da radiação era quantizada.

(b) o campo elétrico da radiação emitida oscilava somente no modo fundamental.

(c) os osciladores na parede da cavidade possuíam energias com valores discretos.

(d) os osciladores na parede da cavidade oscilavam somente no modo fundamental.

Faça a escolha correta e justifique: Na radiação do corpo negro, a energia média de um oscilador depende da frequência de oscilação, segundo Planck. É correto afirmar que:

(a) a energia média independe da temperatura.

(b) o oscilador não emite radiação no modo fundamental.

(c) a intensidade da radiação é quantizada.

(d) os osciladores na parede da cavidade oscilavam com energias discretas

A superfície do Sol está a uma temperatura de , enquanto a superfície da supergigante vermelha Betelgeuse está a uma temperatura de .

Sabendo que a potência irradiada por Betelgeuse é vezes a potência irradiada pelo Sol, determine a razão entre o raio de Betelgeuse e o raio do Sol.

Admita que as duas estrelas possam ser tratadas como corpos negros.

Considere o uso da lei de Wien () valido aproximadamente para a superfície de um corpo. Admita a temperatura dessa superfície .

Determine o comprimento de onda dessa radiação. Diga se está na faixa do visível ().

O gráfico abaixo representa a emitância espectral (distribuição de intensidade) de um corpo negro como função do comprimento de onda.

É dada apenas a escala do eixo de comprimento de onda em . Faltou colocar no gráfico a unidade da escala do eixo da distribuição de intensidade.

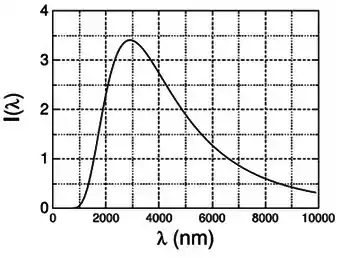
1. Calcule a intensidade total irradiada por esse corpo.
2. Calcule aproximadamente a intensidade irradiada na faixa de comprimentos de onda entre e .
3. Caso a temperatura do corpo seja dobrada. Determine o comprimento de onda do máximo da nova curva e a intensidade total irradiada.

Um filamento cilíndrico com comprimento 𝑙=20 𝑚𝑚 e raio 𝑟=0,05 𝑚𝑚 é submetido a uma temperatura de 𝑇=5000 𝐾 através de uma corrente elétrica. Admita que esse filamento se comporta como um corpo negro e emite radiação isotropicamente.

1. Calcule a potência total irradiada pelo filamento
2. Obtenha o comprimento de onda associado à máxima potência radiada
3. Determine o número de fótons irrradiados pelo filamento a cada segundo. Considere o comprimento de onda médio é de 550 nm

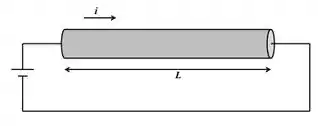
Um resistor cilíndrico de raio e comprimento transporta uma corrente (figura abaixo) e tem potência dissipada dada por O resistor irradia como um corpo negro, emitindo radiação eletromagnética apenas pela sua superfície lateral. Encontre a expressão para a temperatura na superfície lateral do resistor.

Uma estrela esférica de raio e com temperatura emite radiação térmica como um corpo negro.

a) Calcule a quantidade de massa perdida pela estrela durante um intervalo de tempo (expresse sua resposta em termos da constante de Stefan-Boltzmann, de , , e ).

b) Um laboratório na Terra observa que o comprimento de onda do máximo da distribuição de radiação térmica da estrela é . Supondo que a estrela esteja se afastando da Terra com velocidade , calcule sua temperatura, como função de , , e da constante de Wien .

Considere o uso da lei de Wien válido aproximadamente para a superfície das estrelas. Antares é uma gigante luminosa com temperatura de superfície próxima de 3000K. Determine a cor aproximada de Antares.

A superfície de uma estrela tem área de e emite watts. Qual é o comprimento de onda que corresponde ao máximo da distribuição de intensidades da luz emitida por essa estrela?

Aproxime a radiação da estrela pela de um corpo negro.