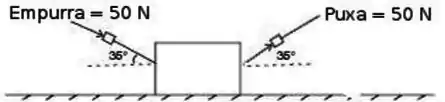
Um estudante empurra uma caixa de sobre o chão a uma velocidade constante. Ele empurra com uma força de que faz um ângulo de em relação à horizontal, como mostrado no diagrama abaixo, à esquerda. Se ao invés de empurrar a caixa, o estudante passa a puxá-la mantendo a força no mesmo ângulo e mesmo módulo, como indicado à direita da figura, o que acontecerá com a força de atrito?
a) Ela deve aumentar.
b) Ela deve diminuir.
c) Ela deve permanecer a mesma.
d) Irá aumentar se a velocidade for maior do que .
e) Irá aumentar se a velocidade for inferior a .
Passo 1
Decompondo as forças no eixo e obtemos:
Como o bloco não tem movimento na vertical, a força resultante na vertical será nula.
Aplicando na Força empurrando:
Aplicando na Força puxando:
Agora temos que lembrar que a força de atrito dinâmica é dada por:
Aplicando as forças normais que achamos vamos ter:
Já deu para perceber que a força de atrito diminuiu quando o estudante resolveu puxar em vez de empurrar, mas vamos calcular a razão entre as forças de atrito para ter certeza.
Essa razão é menor do que , logo a força de atrito diminuiu.
Resposta
Alternativa