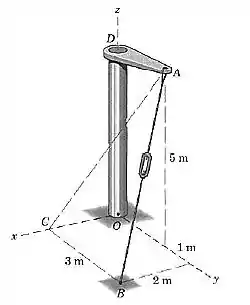
O tensionador é apertado até que a força trativa no cabo valha Determine a expressão vetorial para a força trativa , como uma força atuando no elemento . Ache também o módulo da projeção de ao longo da linha
Passo 1
A força age no elemento , ou seja, no ponto Como a força é trativa, ela deve apontar de para .
Assim, o ponto é o ponto inicial e o final.
Podemos escrever a força trativa como:
Então, devemos achar esse vetor normalizado .
Passo 2
Pela figura do enunciado, o ponto é dado por:
E por:
Assim:
Assim:
Assim, a força pode ser escrita assim:
Passo 3
Pra gente achar a projeção da força em , primeiro temos que definir o vetor unitário que representa essa direção. Nós já sabemos quem é o ponto , precisamos só definir o ponto
Assim:
Então:
Passo 4
Para achar a projeção, basta fazer o produto escalar entre a força e o vetor que define a direção
Veja só: Com isso, nós achamos o módulo do vetor. E qual é a direção? A direção , claro. Então: