Observe a seguinte estatística descritiva referente a uma determinada amostra:
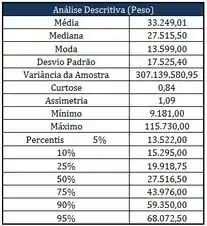
Com relação à estatística descritiva acima, responda as perguntas abaixo:
- Qual o coeficiente de variação da amostra?
- Qual a amplitude máxima da amostra?
- Assimetria positiva indica que existem mais valores altos do que baixos? Sim ou não?
- O que o coeficiente de curtose desta amostra nos permite dizer com relação a uma Normal?
- O que o percentil de desta amostra nos permite dizer?
- Qual é o valor que se repete mais vezes da amostra?
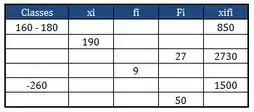
- Na tabela abaixo, temos o diagrama de frequência de uma de elementos onde: os intervalos são iguais; é o ponto médio de cada classe (intervalo); frequência absoluta simples; frequência cumulada. Preencher os espaços vazios do diagrama de frequência.
Passo 1
(a)
Coeficiente de variação é aquela fórmula, desvio padrão dividido pela média. Tudo isso tá na tabela, só dividir.
Passo 2
(b)
Amplitude máxima é o maior valor menos o menor valor, tranquilo, tudo na tabela de novo.
Passo 3
(c)
Não, assimetria positiva quer dizer que a média é maior que a mediana, isso significa que temos mais valores baixos do que altos.
Passo 4
(d)
Nossa curtose é positiva, o que simboliza uma curva platicurtida, aquela mais achatada, lembra? Tem menor curtose que a Normal, comparativamente.
Passo 5
(e)
Nos permite dizer que dos valores da amostra estão abaixo de .
Passo 6
(f)
O valor que mais se repete é a nossa moda, que pode ser vista na tabela.
Passo 7
(g)
Vamos devagar, completar as classes é izi, as classes são todas do mesmo tamanho.
Se a primeira classe vai de , então todas as classes tem amplitude de , só ir completando.
Com isso, completar os também é tranquilão, são os pontos do meio da classe.
Na classe que já ali, , teremos:
Completando esses dois ficamos assim:
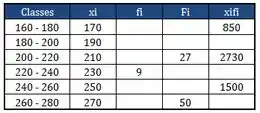
Passo 8
Agora podemos pensar que conhecemos alguns e alguns , então podemos tirar os facilmente.
Do mesmo jeito, conhecemos o e o de uma classe e podemos conhecer o só multiplicar.
Ficaria assim:
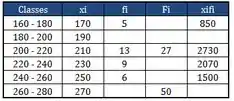
Passo 9
Agora vamos lá, na coluna do eu vou somando os valores de das classes anteriores, concorda?
Então por exemplo, ali a partir do , posso somar e depois ... descobrindo o das classes e , respectivamente.
Hmmm, se o próximo é , consigo descobrir o da última classe que estava faltando também, cert?
E com esse descubro o , multiplicando:
Fiz muita coisa, vamos ver como ficou...
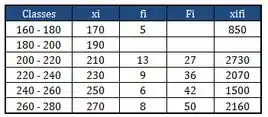
Passo 10
Falta um da coluna que é de boas, só você lembrar que o somatório dessa coluna tem que ser , que é o total de elementos.
E então calculamos:
O primeiro é igual ao , concorda? Não tem mais nada pra acumular, então o segundo será , que é
Finalmente chegamos à tabela completa:
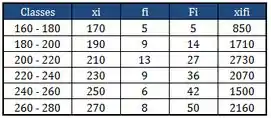
Resposta
Ei, a resposta está no passo a passo :)