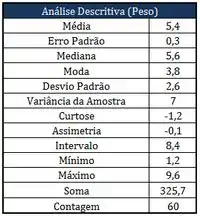
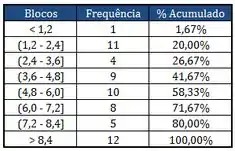
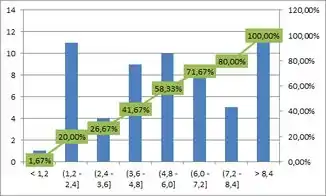
Tomou-se uma amostra de estudantes que fizeram uma prova, e, a estatística descritiva, diagrama de frequência e gráfico de notas da prova estão a seguir:
Com relação aos quadros apresentados da amostra das notas dos estudantes, avalie as seguintes afirmações como Verdadeira (V) ou Falsa (F):
- dos alunos tiraram notas menores ou igual a .
- das notas dos alunos estão entre e .
- Os valores da média e mediana permitem dizer que a distribuição é simétrica.
- Podemos dizer que dos alunos tiraram notas menores ou igual a .
- A assimetria negativa indica que existem mais notas altas e menos notas baixas.
- Podemos dizer que a nota é a que mais vezes acontece.
- O coeficiente de variação conforme a estatística descritiva é igual a .
- Construa o diagrama de Pareto desta amostra, montando em blocos conforme o diagrama de frequência acima (esboce o gráfico).
Passo 1
(a)
Pra saber qual a porcentagem de alunos que tiraram menos ou igual a , basta olhar na tabela acumulada do bloco que termina em . Se você olhar vai ver que é , isso significa que tiraram ou menos.
Afirmação é Verdadeira.
Passo 2
(b)
Vamos ver quantos alunos estão entre as classes e .
No total são alunos, então temos:
Afirmação é Falsa.
Passo 3
(c)
Temos uma assimetria de de acordo com a tabela, então não temos dados simétricos.
Afirmação é Falsa.
Passo 4
(d)
Se você ver o acumulado até o bloco que termina em , vai ver que temos dos alunos. Isso quer dizer que dos alunos tiraram notas menores ou iguais a .
Afirmação é Verdadeira.
Passo 5
(e)
Sim, assimetria negativa quer dizer que a média é menor que a mediana e logo, temos mais notas altas do que baixas.
Afirmação é Verdadeira.
Passo 6
(f)
Não, a nota que mais se repete é a moda, que é informada na primeira tabela.
Afirmação é Falsa.
Passo 7
(g)
Coeficiente de variação é o desvio padrão dividido pela média, então é só fazer conta pra conferir.
Afirmação é Falsa.
Passo 8
(h)
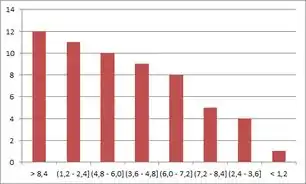
Pra montar o diagrama de Pareto, primeiro colocamos as frequências em ordem decrescente, fica assim:
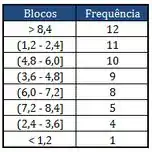
Passo 9
Agora só construir o diagrama de Pareto, que é aquele gráfico com barras da tabela de cima.
Resposta
Ei, a resposta está no passo a passo :)