Os quadros abaixo correspondem aos resultados das notas finais, dos alunos matriculados no período passado na matéria PROBEST 2013-2:
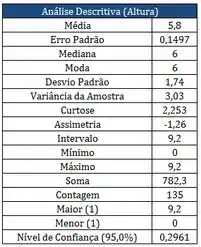
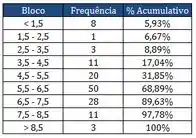
Com relação aos quadrados apresentados, responda as perguntas:
- O total de alunos que tiraram nota final menor ou igual 4,5 foram 11.
- 97,78% dos alunos tem média final menores ou iguais a 8,5.
- Pode-se dizer que a Assimetria “-1,26” é uma curva platicurtica.
- Quais são as medidas de Localização ou Tendência central?
- Quais são as medidas de Dispersão?
- Podemos dizer que a nota final 6,0 é a que mais vezes acontecem.
- O coeficiente de variação conforme a estatística descritiva é igual a 3,33.
- Construa o diagrama de Pareto desta amostra, montando em blocos conforme o quadro do diagrama de frequência. Esboce os gráficos de frequência e % cumulativo, mostrando os valores correspondentes.
V( ) ou F( )
V( ) ou F( )
V( ) ou F( )
V( ) ou F( )
V( ) ou F( )
Passo 1
(a)
Nota final menor ou igual a seria somar todas as frequências até o intervalo .
Então essa é FALSA.
Passo 2
(b)
Primeiro vamos saber o total de alunos:
Agora o número de alunos que passaram com ou menos:
Esses são os que passaram com mais de .
A porcentagem será:
Afirmativa VERDADEIRA.
Passo 3
(c)
A curva ser platicúrtica ou leptocúrtica tem a ver com a curtose. No exercício, temos uma curtose de 2,253. Quando o coeficiente é maior que zero, quer dizer que a curva é leptocúrtica.
Alternativa FALSA.
Passo 4
(d)
As medidas de localização ou centrais são a média e a mediana, que a gente tem na tabela ali em cima.
Passo 5
(e)
Medidas de dispersão são o desvio padrão e a variância.
Outras medidas a gente pode calcular com os dados da tabela, como a amplitude:
Passo 6
(f)
A nota que mais vezes aparece é a moda, que na tabela de cima o exercício diz que é .
Afirmativa VERDADEIRA.
Passo 7
(g)
Coeficiente de variação a gente calcula pela fórmula:
Desvio padrão dividido pela média, que no caso vai ser:
Afirmativa FALSA.
Passo 8
(h)
A tabela que a gente tem é essa:
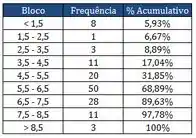
Pra fazer o diagrama de pareto vamos ter que primeiro colocar esses intervalos em ordem decrescente de frequências, do mais frequente pro menos frequente.
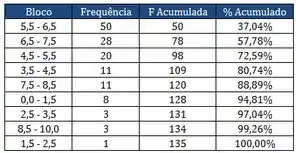
Pra fazer o diagrama de pareto representamos o gráficos de barra das frequências e o gráfico da frequência relativa acumulada.
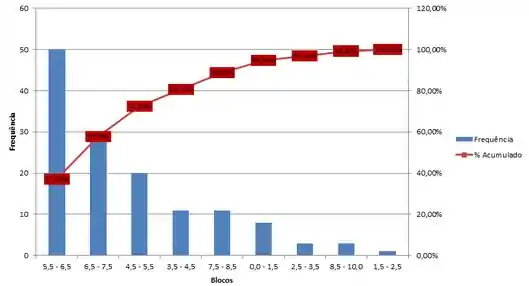
Resposta
Ei, a resposta está no passo a passo :)