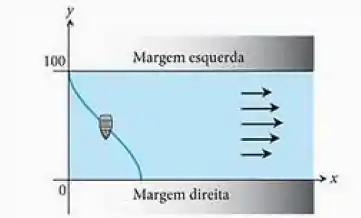
Um rio reto tem de largura. Um barco a remo deixa a margem no instante . A pessoa que está no barco rema a sempre na direção da margem direita. A velocidade do rio em é
- Dado que , qual é a posição do barco no instante ?
- A que distancia rio abaixo o barco atingirá a margem direita?
Passo 1
Vamos lá: queremos achar a posição do barco em relação a margem e o que temos são informações sobre a velocidade do barco em relação ao rio e a velocidade do rio. Temos então que achar a velocidade do barco em relação a margem para então integrá-la e achar a posição do barco em relação a margem!
A velocidade do barco em relação a margem é igual a soma da velocidade do barco em relação ao rio e da velocidade do rio. Isto é, uma pessoa que está parada na margem do rio vê o barco se movimentando com a sua velocidade em relação as aguas do rio, mas também sendo movimentado pela correnteza do rio.
Nossos dados então são:
Substituindo:
Passo 2
Opa, mas ai temos que a velocidade do barco em relação a margem está em função de e sabemos que quando se trata de velocidade, o parâmetro tem que ser o tempo .
Mas, como só tem gente esperta aqui, a gente sabe que
Porque o barco se aproxima da margem, andando sempre na direção , no sentindo negativo, com uma velocidade de , ou seja, a taxa de variação de da distancia em relação ao tempo é de .
Então
Passo 3
Sabemos que , ou seja, no instante o barco está na posição da margem esquerda.
Logo:
Passo 4
Pronto, agora já podemos substituir o na velocidade do barco em relação a margem
Passo 5
Agora sim podemos integrar a velocidade e recuperar a posição do barco em relação a margem
Passo 6
Para descobrir usamos o fato de que , assim:
Logo
Passo 7
Agora queremos descobrir qual será o valor de quando . Para isso, precisamos descobrir em que valor de o barco atinge a posição .
Fazemos:
Passo 8
Por fim, é só substituir no vetor posição para saber qual será o valor da coordenada :