Seja um campo vetorial irrotacional de classe definido em , onde e . Seja a circunferência de raio 1 centrada em e seja a circunferência de raio centrada em , ambas com sentido anti-horário. Suponha que
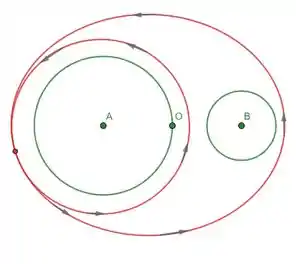
- Expresse como uma combinação linear de e com coeficientes racionais, onde é a curva fechada representada no desenho abaixo:
- Supondo que onde
Determine os valores das constantes reais e .
Passo 1
Fala pessoal! Uma ideia direta e braçal é integrar primeiro em e depois em e montar um sistema em , como abaixo:
De forma que calculando as integrais, nosso problema se reduz a resolução de um sistema linear com duas incógnitas e duas equações.
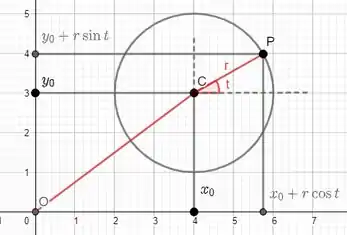
Assim, as circunferências de centro e raio e, ainda, de centro e raio são dadas por:
Com isso, calcularemos as integrais de curva dos campos vetoriais usando:
Porque e apresentam simetria em relação a e respectivamente.
Passo 2
Logo,
Passo 3
E ainda,
Passo 4

Agora, nas outras duas integrais:
Perdemos a simetria, então o cálculo pode ficar complicadinho, mas não deixa de ser uma opção calcular:
Contudo, como forma de encurtar esse cálculo veja que se integrarmos as coordenadas de em relação a e , respectivamente, obtemos funções similares. Isto nos leva a:
Com contínua no interior de . Logo podemos aplicar o Teorema de Green, o qual indica que para funções contínuas em uma região D cujo limite seja C:
Assim,
Tal que:
Onde o operador laplaciano: e a menos de um fator multiplicativo e uma translação é solução fundamental da equação de Laplace, isto é:
Como é fácil verificar:
Assim,
Analogamente, observe que
Com a qual também é contínua no interior de , donde, teremos pelo mesmo raciocínio:
Passo 5
Passo 6
Retornando ao sistema original, temos: