Determine no circuito abaixo usando superposição.
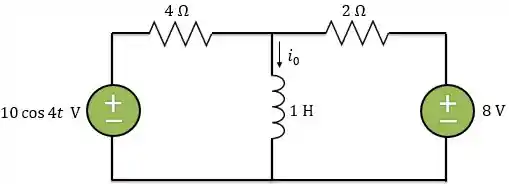
Passo 1
Aplicando o princípio da superposição, a corrente será dada por:
Onde é a contribuição da fonte de tensão alternada e é a contribuição da fonte de tensão CC.
Passo 2
Para determinar , temos que desligar a fonte de tensão CC, ou seja, considerá-la um curto-circuito e passar o circuito para o domínio da frequência.
Logo, o circuito no domínio da frequência é:
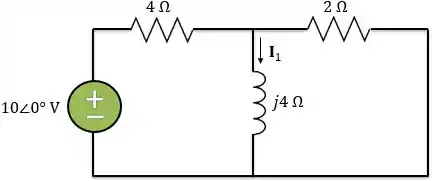
Passo 3
Agora, vamos utilizar a análise nodal:
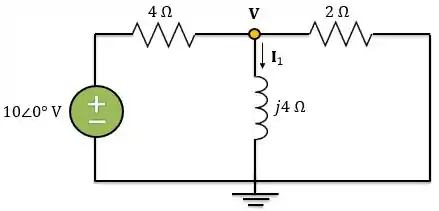
Logo, pela lei de Ohm:
Voltando para o domínio do tempo:
Passo 4
Para determinar , temos que desligar a fonte de tensão CA, ou seja, considerá-la um curto-circuito e considerar apenas a fonte CC. Além disso, temos que lembrar que em regime permanente CC o indutor é um curto-circuito. Portanto, temos que analisar o seguinte circuito:
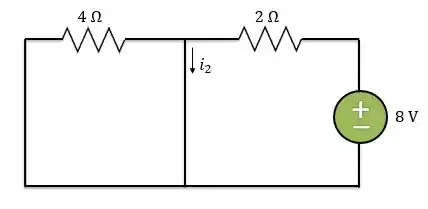
Toda a corrente fornecida pela fonte passa pelo curto-circuito. Logo, não tem circulação de corrente no resistor e será:
Passo 5
Logo, pelo princípio da superposição, a corrente é dada por: