Utilize o método da transformação de fontes para determinar no circuito abaixo:
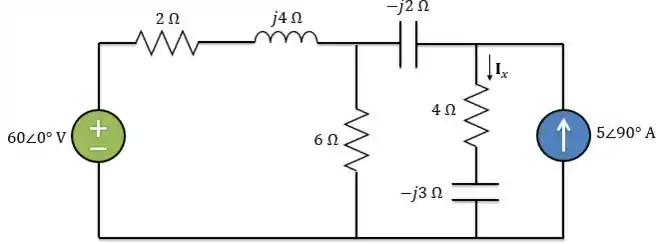
Passo 1
O circuito já está na forma fasorial. Então, podemos partir direto para as transformações de fonte. Primeiro, vamos considerar:
Transformando a fonte de tensão em série com a impedância em uma fonte de corrente em paralelo com , temos que a fonte de corrente terá o seguinte valor:
Portanto, temos o seguinte circuito:
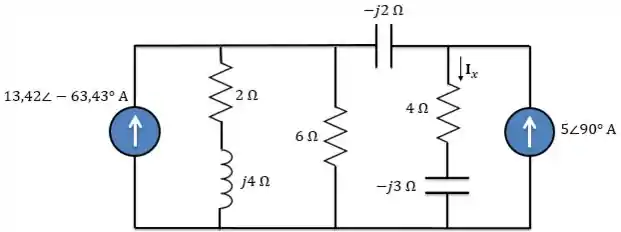
Passo 2
Considerando:
Usando mais uma vez transformação de fontes. Vamos transformar a fonte de corrente em paralelo com em uma fonte de tensão em série com . O valor da fonte de tensão será:
Portanto, o circuito fica assim:
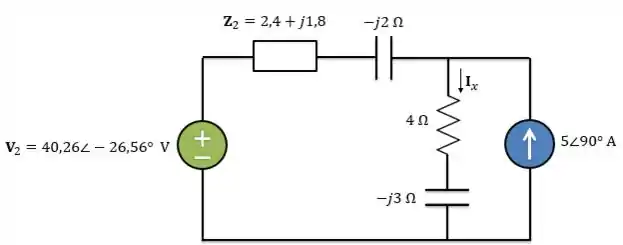
Passo 3
Agora, vamos considerar:
Então, vamos transformar a fonte de tensão em série com em uma fonte de corrente em paralelo com . O valor da fonte de corrente será:
Logo, temos o seguinte circuito:
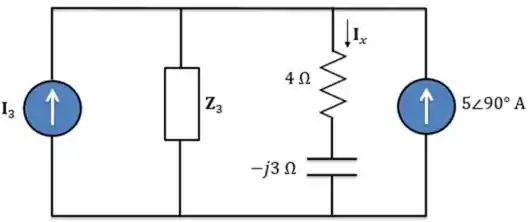
Passo 4
Para terminar, vamos aplicar divisor de corrente: