Usando a transformação de fontes, determine no circuito abaixo:
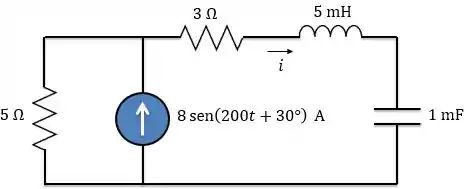
Passo 1
De cara, temos que passar o circuito para o domínio da frequência:
Portanto, o circuito no domínio da frequência será:
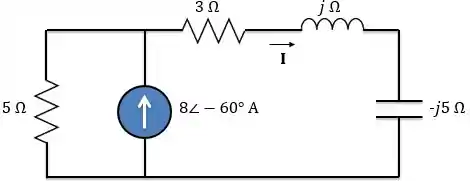
Passo 2
Agora, vamos utilizar transformação de fontes. Transformando a fonte de corrente em paralelo com o resistor de em uma fonte de tensão em série com o mesmo resistor, temos:
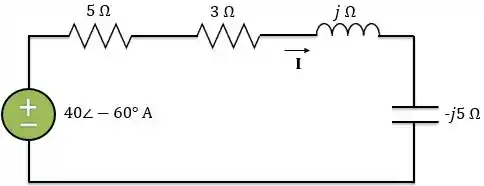
Passo 3
Portanto, a impedância do circuito é:
Aplicando a lei de Ohm encontramos a corrente:
Voltando para o domínio do tempo, temos: