Uma amostra de é colocada em um sistema de resfriamento que remove calor a uma taxa constante. A figura abaixo indica a temperatura da amostra em função do tempo ; a escala do eixo horizontal é definida por . A amostra congela durante o processo. O calor específico da amostra no estado líquido inicial é . Determine o calor de fusão da amostra e o calor específico da fase sólida.
Passo 1
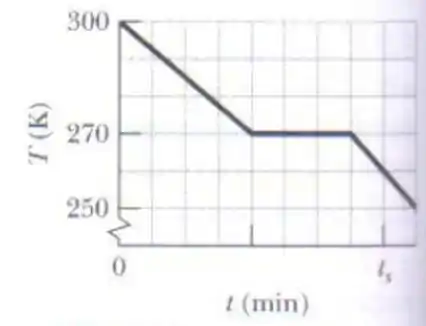
Nesse processo existem três etapas bem definidas a primeira, onde a substância está na fase líquida há e resfriamos até de acordo com o gráfico.
A segunda etapa consiste na mudança de fase da substância, podemos ver no gráfico que a temperatura se mantém em por um tempo até toda a substância ter virado sólido e assim começa a terceira etapa.
A terceira etapa começamos a varia a temperatura da amostra novamente até chegarmos em .
Pelas etapas que acabamos de descrever conseguimos afirmar que
Passo 2
Queremos saber o calor de fusão da amostro, temos calor de fusão na segunda etapa certo? Porém não sabemos quanto de calor foi retidado do gelo, apenas sabemos pelo gráfico que demorou minutos para transformar toda a amostra líquida em sólida.
Como descobrimos que são minutos? , certo? O está a exatos quadrados da origem, então sabemos que cada quadrado vale , sendo assim vimos que a segunda etapa dura 3 quadrados, então chegamos em .
Passo 3
Mas o enunciado disse que a taxa de remoção de calor é constante, então precisamos descobrir o valor dessa taxa para podermos resolver esse item. Mas como descobriremos isso?
Bem, vamos estudar a etapa em que temos tudo. Que etapa é essa? A primeira, certo?
Assim conseguimos saber qual é a quantidade de calor necessária que o sistema remova para variarmos esses
Passo 4
Sabendo que em minutos foram retirados da amostra, podemos descobrir a taxa de remoção de calor do sistema
Passo 5
Agora que temos a taxa de remoção, podemos descobrir quantos joules foi necessário remover da segunda etapa para solidificar toda a amostra. Lembrando que a segunda etapa demorou minutos
Passo 6
Pronto, já temos a quantidade de calor retirada na segunda etapa. Assim podemos calcular o valor do calor de fusão da amostra.
Passo 7
Para descobrir o calor específico da fase sólida vamos estudar a terceira etapa, onde sabemos
Para resolvermos isso precisamos descobrir o quanto de calor foi retirado do sistema, como já calculamos a taxa de remoção de calor, essa tarefa é tranquilo
Passo 8
Agora é só substituir na fórmula de calor sensível que já conhecemos