UFF, Volta Redonda, Cálculo Diferencial e Integral II, Listas Cálculo Diferencial e Integral II - Lista 2 - Integral Tripla - 2019.1, Questão 3.
3-Calcule o volume do sólido limitado superiormente pela esfera e inferiormente pelo cone .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema estamos interessados em obter o volume do solido limitado pela esfera e acima do cone .
Como obtemos esse volume? 👀
Perceba que há uma simetria esférica no problema, então temos que converter as coordenadas cartesianas para as coordenadas esféricas.
Entendeu? Bora começar! 😊
Passo 2
Sabemos que o cálculo de volume a partir de uma integral tripla é dada por .
Se analisarmos a região de integração, temos
A partir dessa região, vemos que o sólido é o cone limitado superiormente pela esfera de raio .
Portanto, para os limites de integração em coordenadas polares
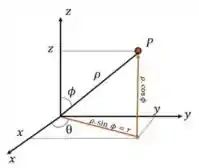
Vemos que varia de a , de a e de a .
Com isso, nossa integral volumétrica será dada (sem esquecer do jacobiano “”) por
Tranquilo até aqui? 😁
Passo 3
Integrando com relação a , temos
Aplicando os limites de integração...
Integrando o resultado em relação a pelo teorema fundamental do cálculo.
Aplicando os limites de integração...
E por fim, integrando o resultado com relação a
Aplicando os limites de integração
Com isso, temos que isso, temos que
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
