Encontre o valor médio de sobre a região delimitada por
Passo 1
Temos uma região um pouco mais complicada dessa vez ne? Mas não se assuste, o passo a passo vai ser o mesmo, vamos entender um pouco o que significa esse que ele nos deu.
A nossa primeira equação trata-se da equação de um cilindro de raio , já nos dá uma ideia de que teremos que fazer mudança de variáveis para coordenadas cilíndricas, então se isso não está mt bem fixado dá uma olhada nos exercícios desse tipo.
Nosso cilindro vai ser limitado pelos planos e , fica mais ou menos assim:
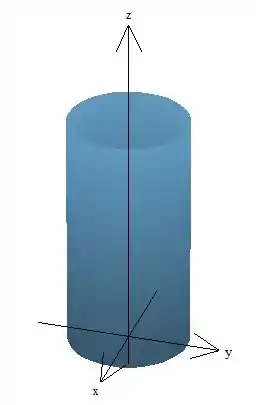
O volume de um cilindro é dado pela fórmula
Lembrando da nossa equação do valor médio temos que
Precisamos calcular então o volume de e os limites dessa integração mudando as variáveis de para
Passo 2
Vamos identificar os limites de integração da nossa região . Perceba que, por ser um cilindro, é mais fácil transformar em . Teremos então:
O jacobiano dessa mudança de variável é:
Pela equação do cilindro:
Portanto os nossos limites de integração serão:
Passo 3
Para calcular o volume do cilindro podemos usar a fórmula dada no passo 1:
OBS: Se você não se lembrasse da fórmula do cilindro, poderia descobrir o volume usando a seguinte integral tripla:
Onde e tem os limites de integração calculados no passo 2.
Passo 4
Agora vamos juntar tudo na integral e resolver, tome muito cuidado para não esquecer nenhum termo nessa parte!
Quando mudamos de variável, nosso tem que ser transformado em um
Colocando tudo na integral:
Integrando em :
Integrando em :
Finalmente, integrando em :