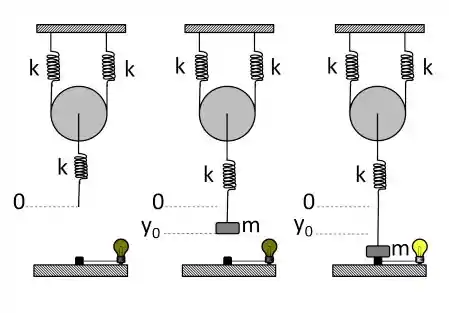
Considere um sistema como o da figura ao lado, composto pro três molas idênticas( com constantes de massas desprezíveis e uma polia, também de massa desprezível. Inicialmente o sistema está em equilíbrio na posição Em um determinado momento, uma massa é conectada a uma das molas, deslocando o sistema do valor Logo desta massa há um dispositivo sensível ao toque que acende uma lâmpada de cada vez que é tocado pela massa. Despreze quaisquer efeitos de atrito no sistema. Supondo que a distância entre a posição de equilíbrio da massa e a superfície do dispositivo sensível ao toque é de e que, para dar início ao movimento, você simplesmente encosta a massa no dispositivo e libera o sistema, calcule:
- A posição de equilíbrio
- A equação do movimento resultante da massa
- A solução da equação do movimento da massa
- O valor que deve ser escolhido para a massa para que a lâmpada acenda uma vez a cada segundos.
- O trabalho realizado sobre o sistema em equilíbrio para dar início ao movimento descrito no item .
Passo 1
a):
Bom galera, aqui a gente precisa reconhecer que ali tem uma associação de molas: Tanto em paralelo quanto em série.
Primeiro há uma associação em paralelo. Em associações assim, a gente soma as constantes das molas:
Depois existe uma associação em série. Nesse caso, usamos a soma dos inversos:
Bom, pra achar agora a posição de equilíbrio , basta a gente perceber que na posição de equilíbrio, a mola equilibra o peso. Assim, esse é a elongação que a mola possui e que gera essa força de equilíbrio. Assim:
Passo 2
b):
Como estamos falando de um MHS não amortecido, a equação diferencial do movimento segue o modelo dos MHS, que a gente acha usando a segunda lei de Newton(como sempre!):
Sendo :
Ai a gente pode lembrar da letra a) (
Passo 3
c):
Usando a equação de b), podemos fazer a substituição . Então a solução pra segue o modelo padrão e é:
Lembrando que:
Precisamos achar e .
Bom, o enunciado nos diz que a distância entre a posição de equilíbrio e a mesa é cerca de .Vamos considerar que a massa inicia seu movimento colada com a mesa. Então, considerando como zero a posição de equilíbrio, a massa inicia seu movimento na posição de Então:
Derivando
Como ela inicia o movimento em repouso, . Então:
Substituindo na equação da amplitude:
Então a equação vai ser:
Como
Show! Agora é só voltar para
Passo 4
d):
“Uma vez a cada segundos.” Significa que o período será . Po, mas a gente sabe muito bem as relações entre período e velocidade angular:
Então:
Passo 5
e):
Bom, o trabalho a gente costuma fazer assim: , não é mesmo? NÃAAO!
A gente ate faz isso, mas vamos fazer de uma forma simples. Da mecânica, a gente sabe que o trabalho de uma força é igual à variação de energia potencial da mola:
Sendo e :
Resposta
a):
b):
c):
d):
e):