Uma barra de comprimento ocupa uma região onde há um campo magnético constante (estacionário e uniforme) . A barra gira com velocidade angular , em torno de um ponto fixo em uma de suas extremidades, em um plano perpendicular ao campo. Qual é o módulo da tensão ou da diferença de potencial que acaba se estabelecendo entre as extremidades da barra?
Passo 1
Desenhando a situação, lembrando que ele não deu o sentido do campo , somente deu a direção que é perpendicular ao plano da barra, vamos chutar um sentido qualquer para este vetor:
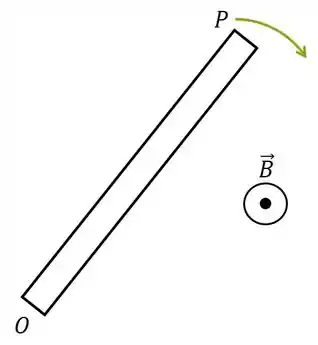
Vamos estudar as partículas positivamente carregadas da barra para não nos preocuparmos com sinal. Elas vão ser aceleradas pela força magnética e vão se mover para alguma das extremidades da barra:
Passo 2
Vamos agora tentar avaliar pra onde vai ser o sentido da força. Como cada partícula tem uma velocidade , lembrando que a velocidade é tangente à trajetória, sabemos que a força aponta para a extremidade :
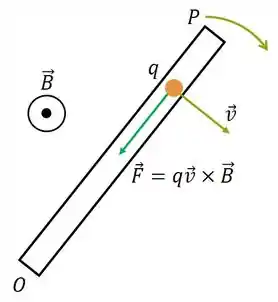
Passo 3
Agora vamos ter um acúmulo de cargas positivas na extremidade da barra. Por conta desse acúmulo de cargas de mesmo sinal, elas começam a se empurrar no sentido oposto por causa da força elétrica, até que num dado momento a força elétrica fica tão grande que elas param de ser empurradas para qualquer lado pois entraram em equilíbrio.
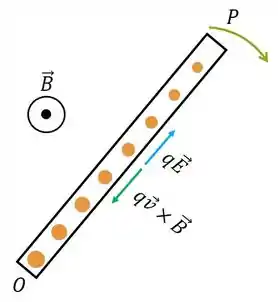
Ou seja, as forças opostas se igualam. Seja o acúmulo de cargas em um ponto arbitrário. Segue que os módulos das forças elétrica e magnética se igualam:
Onde é a velocidade em um ponto arbitrário.
Passo 4
Sabemos que, por aquela relação matemática que a gente nunca lembra mas eu tenho a Wikipédia aqui aberta, a velocidade é igual à:
Como temos o campo elétrico, podemos calcular a diferença de potencial:
Como o enunciado quer o módulo, ignoramos sinais. Pegando uma trajetória retilínea entre as extremidades, temos:
A variável , portanto, varia ao longo da barra, e vai do ponto fixo até a outra extremidade.
Passo 5
Substituindo o campo elétrico na integral:
Segue que:
Obs.: Essa questão é considerada difícil!
Resposta
Letra d