Na figura abaixo, um elétron acelerado a partir do repouso por uma diferença de potencial entra no espaço entre duas placas paralelas, separadas por uma distância , entre as quais existe uma diferença de potencial .

A placa inferior está a um potencial menor. Despreza o efeito de borda e suponha que o vetor velocidade do elétron é perpendicular ao vetor campo elétrico na região entre as placas.
Em termos dos vetores unitários, qual é o campo magnético uniforme para o qual a trajetória do elétron na região entre as placas é retilínea?
Passo 1
Então, primeiro vamos resumir esse enunciado: temos um elétron que é acelerado até entrar numa região que apresenta campos cruzados. Ele quer que a gente calcule o campo magnético para o qual o elétron não sofrerá desvio.
São dados: , , e a informação de que o vetor velocidade do elétron é perpendicular ao vetor campo elétrico na região entre as placas.
Passo 2
Beleza, vamos começar calculando o módulo do campo magnético. Para que a trajetória do elétron não sofra nenhum desvio, vimos que é necessário que:
O campo elétrico entre as placas é dado por:
Onde:
Portanto:
O problema é que não sabemos quanto vale a velocidade e não podemos usar essa mesma relação acima para a porque não sabemos a distância em que o elétron foi acelerado por esse potencial, então vamos ter que ir por outro caminho.
Passo 3
Para determinar a velocidade com que o elétron chega na região entre as placas, vamos usar a energia cinética do elétron. Oi?! Como assim?!
Se liga, a variação de energia cinética do elétron deve ser igual ao trabalho realizado sobre ele.
Logo:
Como o elétron parte do repouso, sua velocidade inicial é nula, portanto:
Onde:
Portanto:
Passo 4
Agora sim! O módulo do campo magnético será:
O próximo passo é determinar a direção e sentido do campo magnético... pra isso, vamos fazer uma análise vetorial.
Passo 5
Sabemos que o elétron se move na no sentido . Além disso, o enunciado disse que a placa superior possui um potencial maior, isso significa que o campo elétrico está no sentido , como mostra a figura abaixo.
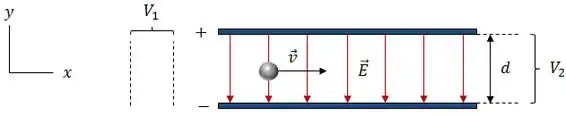
Como se trata de um elétron (carga negativa), a força elétrica sobre ele estará apontando no sentido contrário do campo elétrico, logo, no sentido .
Já sabemos que, para o elétron não sofrer nenhuma deflexão na sua trajetória:
Isso quer dizer que a força magnética estará apontando no sentido .
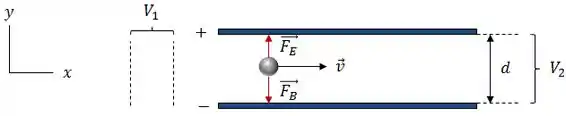
Cara, vou ser sincero contigo... acho muito mais tranquilo usar a regra da mão direita aqui...
Nós sabemos que:
Assim, basta colocar o polegar no sentido de e o seu indicador no sentido de e vemos que o campo magnético deve estar no sentido . Só que como o elétron tem carga negativa, nosso resultado será o contrário, e o campo magnético na verdade estará no sentido .