Encontre uma parametrização para a superfície obtida girando-se a circunferência abaixo em torno do eixo :
Passo 1
Já sabemos que, quando aparecer essa história de rodar uma função em torno de algum eixo, estamos tratando de superfície de revolução né? Essa está rodando em torno do eixo , portanto vamos colocar aquele fator de giro nos eixos e .
O gráfico da nossa superfície de rotação é esse aqui:
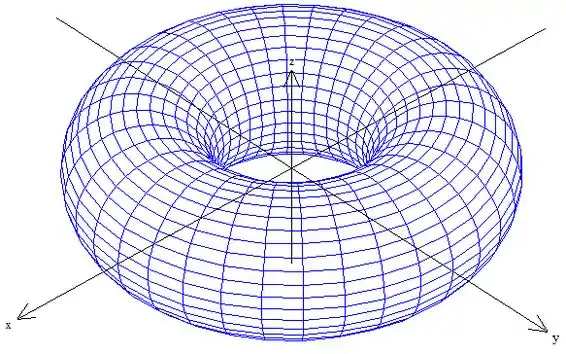
Passo 2
Para conseguir parametrizar a superfície, precisamos antes obter nosso e certo? Vamos ver a nossa equação da circunferência inicial:
Pela relação fundamental trigonométrica
Temos que
Como é o círculo inteiro que está rodando, temos que
Passo 3
Agora só falta substituir tudo na fórmula! Como rodamos no eixo , o fator de giro entra nos eixos e , e a nossa parametrização fica assim: