1) Parametrize as superficies abaixo, indicando o domínio dos parâmetros:
: superfície de revolução obtida girando a curva , com , em torno do eixo .
Passo 1
Parece que temos variável demais no problema né? O que o enunciado quis dizer é que, depois de escolhermos um valor de , o raio tem que estar entre e . Portanto, de variável mesmo só temos e na equação! Faz mais sentido agora né? e são constantes!
Já sabemos que, quando aparecer essa história de rodar uma função em torno de algum eixo, estamos tratando de superfície de revolução né? Essa está rodando em torno do eixo , portanto vamos colocar aquele fator de giro nos eixos e .
O gráfico da nossa superfície de rotação é esse aqui:
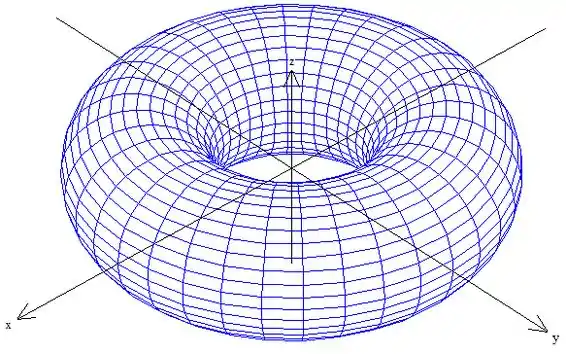
Passo 2
Para conseguir parametrizar a superfície, precisamos antes obter nosso e certo? Vamos ver a nossa equação da circunferência inicial, lembrando que e são constantes:
Associando à relação fundamental:
Temos que
E que
Como é o círculo todo que está rodando, temos que
Passo 3
Agora só falta substituir tudo na fórmula! Como rodamos no eixo , o fator de giro entra nos eixos e , e a nossa parametrização fica assim: