1) Parametrize as superfícies abaixo, indicando o domínio dos parâmetros:
d) cone gerado pela semireta , , girando-a em torno do eixo .
Passo 1
Sugiro sempre a você em casos de parametrização como esse, fazer um esboço da superfície que você está trabalhando. Nem precisa ser perfeito, pois é mais para te dar uma noção do que fazer mesmo.
No nosso caso, o que devemos fazer é pegar essa reta no plano ...

E girá-la ao redor de :
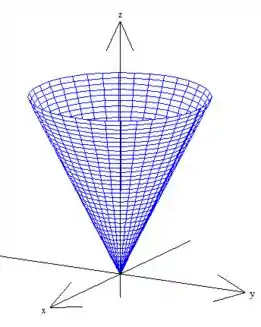
Formando ao pedaço de cone pedido! (note que embora tivemos que colocar um fim, o cone do problema não tem um, então ele vai crescendo indefinidamente )
Passo 2
Uma superfície como essa, foi gerada com uma revolução, logo a parametrização que devemos utilizar é a parametrização que chamamos de parametrização de superfícies de revolução. Bem sugestivo, neh? kkkkkk
Para essa superfície, como você já sabe, primeiro parametrizamos a curva que deu origem, no caso, a reta:
Se chamarmos ... então ...
Logo a parametrização da curva é...
Repare que ficaram uns vácuos ali! Isso porque a uma curva precisa de uma única variável e a superfície de duas, bora encontrar a segunda?
Passo 3
Bem, o segundo parâmetro é o ângulo que chamamos de fator de giro. Como no caso estamos girando ao redor de , ou seja, no plano ...
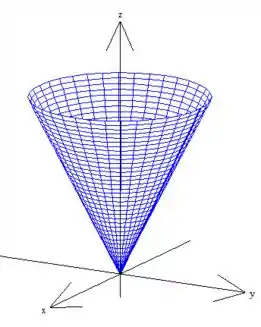
Devemos colocar uma correção com um cosseno e um seno em e . O cosseno, se quisermos o ângulo saindo do eixo no sentido anti-horário como no desenho acima, deve ser necessariamente o e o o seno:
Então a parametrização fica...
Como tem um na frente do seno, tem que ter na frente do cosseno também:
Eis a parametrização!
Passo 4
Ok, agora nos falta a segunda parte do problema que é encontrar o domínio dos parâmetros: onde eles estão variando.
Bem, o ângulo gira no plano ao redor do eixo :
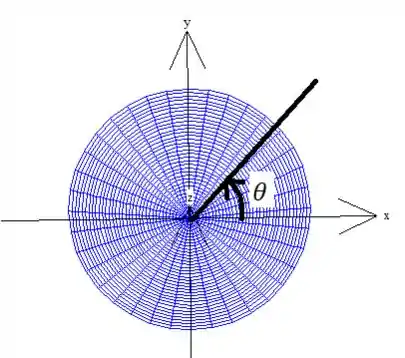
Como pode ver na projeção da superfície no plano , precisamos de um dando uma volta completa:
Enquanto isso, o que representa o raio dessa projeção, pelo fato de o cone não ter fim, o raio não tem um limite superior, apenas o inferior que é o (raio não pode ser negativo)...
Podemos omitir essa notação do infinito e dizer simplesmente que...