1) Parametrize as superfícies baixo, indicando o domínio dos parâmetros:
f) parte do cilindro , que fica entre e .
Passo 1
Sugiro sempre a você em casos de parametrização como esse, fazer um esboço da superfície que você está trabalhando. Nem precisa ser perfeito, pois é mais para te dar uma noção do que fazer mesmo.
No nosso caso, estamos lidando com a parte do cilindro deslocado, pois...
Completando quadrado:
É um cilindro deslocado em de raio :
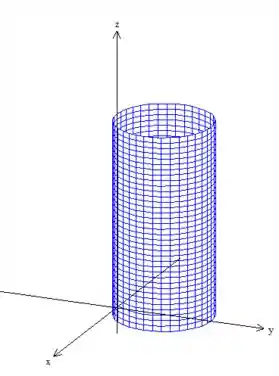
Mas queremos apenas a parte do cilindro que está acima do (palno ) e abaixo do paraboloide:
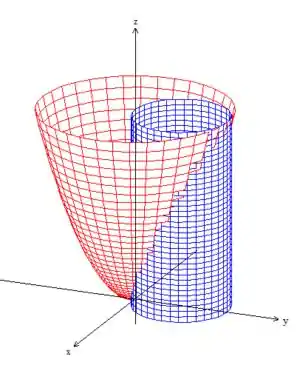
Passo 2
Bem, estamos trabalhando com um pedaço de cilindro, então nada mais justo que utilizar uma parametrização “prima” das coordenadas cilíndricas (lembre-se que o cilindro está deslocado em ):
Agora tome muito cuidado! Uma superfície, mesmo no espaço, tem duas dimensões, certo? Então ela precisa sempre de dois parâmetros para descrevê-la. No nosso caso, é só o ângulo e o próprio , esse desaparece virando o raio do cilindro que estamos trabalhando...
Logo a parametrização é...
Ou, com uma anotação um pouco mais elegante do ponto de vista da matemática...
Passo 3
Ok, agora nos falta a segunda parte do problema que é encontrar o domínio dos parâmetros: onde eles estão variando.
Bem, como a parametrização é prima das coordenadas cilíndricas, o ângulo gira no plano ao redor do eixo do cilindro:
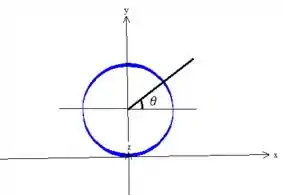
Como pode ver na projeção da superfície no plano , precisamos de um dando uma volta completa:
Passo 4
Enquanto isso, o varia entre o plano e o paraboloide:
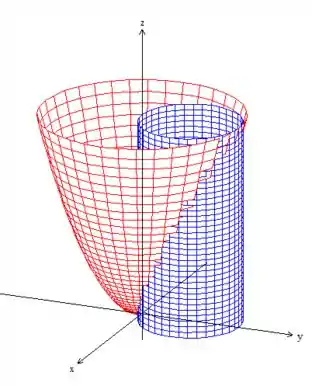
Trocando os termos e pelos parâmetros...
Como ...