Calcule
Onde é a curva:
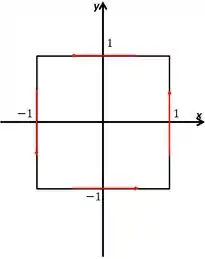
Passo 1
Primeiramente, vemos que nossa integral está escrita na forma:
Então:
E nossa curva pode ser dividida em quatro partes de forma que . Então vamos começar dando nome aos bois:
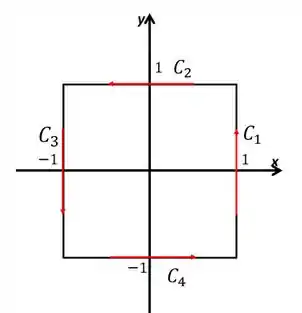
Cada uma dessas curvas são retas. Então vamos ter algo do tipo:
As curvas são bem parecidas e tal, mas vamos calcular uma por uma pra ter certeza e não confundir nada.
Passo 2
Começando por , lembramos que a fórmula que vamos usar é:
Passo 3
A parametrização dela vai ser:
Passo 4
então é só calcular o vetor tangente:
Passo 5
E jogar na fórmula, pra fazermos o produto escalar:
É uma integral meio complicada, mas pra quem não lembra:
Passo 6
Agora repetimos o método para :
Vamos ver como fica o vetor tangente:
Bem parecido com o outro, mas olha como a integral fica diferente:
Essa é mais fácil, pelo menos:
Passo 7
E mais uma vez, aplicamos a fórmula pra :
E o vetor tangente:
Jogando na integral:
Opa, ja vi isso antes, né? Haha
Passo 8
E, por último, finalmente, :
O que vem agora, adivinha? Isso, vetor tangente:
E a integral:
Que, como já vimos:
Passo 9
Pra terminar, só somar tudo:
Achou estranho? Bem, mas é isso mesmo, pode confiar!