Considere a integral de linha
Onde é a fronteira da região do primeiro quadrante limitada pelas circunferências e , orientada no sentido anti-horário e é o campo vetorial definido por
Calcule Essa integral pela definição de integral de linha.
Passo 1
Temos que entender como é a região que ele falou. Repara que a região vai ser entre as circunferências de raio e , e limitada por e porque está no primeiro quadrante. Então a região fica assim
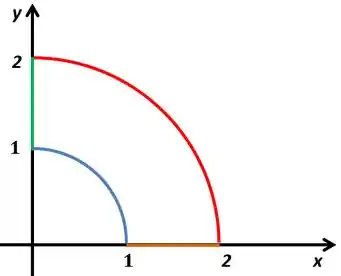
Como ele quer no sentido anti-horário vamos ter o seguinte sentido das 4 curvas
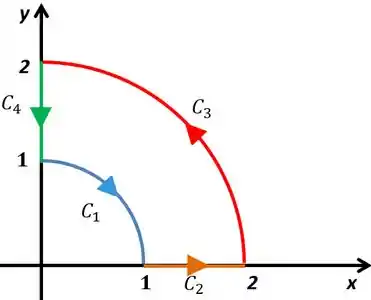
Para fazer a integral de linha vamos ter
Passo 2
Vamos começar com , vamos fazer a parametrização da circunferência de raio
Na verdade temos que pegar a integral com o sinal trocado né? Desse jeito ele está rodando no sentido contrário ao longo da circunferência.
Agora queremos a derivada
A integral vai ficar
Lembrando que
Passo 3
Vamos agora para , nela só p valor de vai variar, que vai de à , então a parametrização fica
Com
Vamos a derivada da parametrização
A integral vai ficar
Passo 4
Vamos para , vamos fazer a parametrização da circunferência de raio
Aqui ele está rodando no sentido certinho
Agora queremos a derivada
A integral vai ficar
Lembrando que
Passo 5
Vamos agora para , nela só o valor de vai variar, que vai de à , então a parametrização fica
Com
Na verdade temos que pegar a integral com o sinal trocado né? Desse jeito ele está rodando no sentido contrário ao longo da reta.
Vamos a derivada da parametrização
A integral vai ficar
Passo 6
Vamos ter
Então