- Calcule a componente do centro de massa do sólido dado por , , , , se a densidade no ponto é inversamente proporcional ao quadrado da distancia do ponto à origem.
Passo 1
Bem, o do centro de massa se calcula por
Onde é a função densidade do sólido e a .
Mas aí surge duas duvidas não é verdade?!
- Quem é o sólido que estamos trabalhando?
- Quem é a função ?
Passo 2
Vamos começar aqui respondendo a primeira pergunta... Quem é o sólido que estamos trabalhando?
Cara, não pira, pois esse sólido é e não é complicado ao mesmo tempo, porque precisamos apenas saber de duas superfícies basicamente, as outras duas são basicamente as mesmas saca?
Note que é uma esfera, mas ela está deslocada. Se levarmos para sua forma original de esfera completando quadrado...
Viu só? Uma esfera de raio e com o centro deslocada em :
também é uma esfera, mas...
de raio e centrada unidades pra cima.
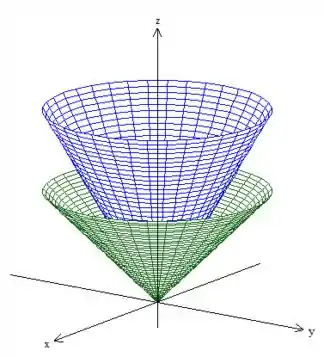
é um cone que delimita em baixo (representado em verde), , um cone que delimita em cima:
Eis o sólido !:)
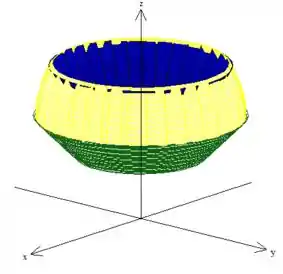
Passo 3
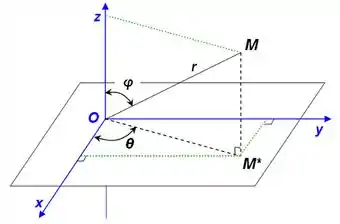
Bem, estamos trabalhando dentro de uma esfera, então... Nada mais justo utilizarmos as coordenadas esféricas, onde
O jacobiano dessa mudança é
E uma equação que é bastante útil é a equação da esfera:
Nunca devemos sair de uma mudança enquanto não encontramos onde essas novas variáveis estão variando. Bora?
Passo 4
Vamos começar aqui pelo mais fácil! Pelo ângulo , afinal de contas esse ângulo está dando uma volta completa, então logo ele só pode estar girando de até .
Em relação ao ângulo , pow, repare que ele está variando do cone superior, , ao cone inferior
Substituindo as coordenada polares nas equação dos cones... vamos ver no que dá (Veja em relação )
Passando esse pro lado de lá e esse pro lado de cá...
Sacou?
Em relação ao outro cone,
logo
Passo 5
Só nos falta o , e pow, note que o , entra na esfera menor, e sai na esfera maior
A esfera menor tem como equação. De modo análogo ao passo anterior, substituímos as polares para ver no que vai dar. Veja:
Enquanto que a esfera maior...
logo
Passo 6
Wow! Yeah! A segunda pergunta...
- Quem é a função ?
Bem... O próprio enunciado disse que a densidade é inversamente proporcional ao quadrado distancia de um ponto a origem. A distância a esse ponto é
logo
onde é a constante de proporcionalidade, ok?
Passo 7
Podemos então agora montar a primeira integral que precisamos para matar o nosso problema:
Trocando para as coordenadas esféricas não esquecendo do Jacobiano:
Integrando o de dentro...
substituindo e simplificando...
Para calcular essa integral do meio aqui, fazemos uma substituição simples...
Não se esqueça de trocar os limites...
Retornando à integral...
ganhamos
Passo 8
Indo então para a próxima integral... (não desista, pois ainda precisamos da massa hehe)
Trocando para as coordenadas esféricas não esquecendo do Jacobiano:
E repetindo todo o processo de resolução de integrais triplas...
ganhamos...
Passo 9
Voltando para a fórmula e substituindo...
dividindo ganhamos...