Calcule a massa da região , com função densidade .
Passo 1
O problema pede que calculemos a massa do sólido delimitado pelas superfícies acima, sabendo que sua densidade é dada por . Nós sabemos que:
Onde é o diferencial de massa e o de volume. Integrando ambos os lados na região em que o sólido está contido, temos que:
Passo 2
Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido. Temos uma esfera de raio centrada em :
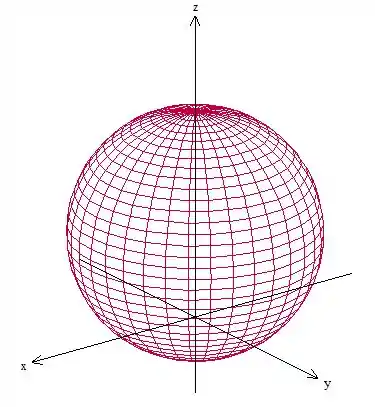
A região do problema é o que está dentro da esfera e acima do plano , beleza?
Passo 3
Como a região é limitada por uma esfera, vamos utilizar coordenadas esféricas:
Na verdade, para facilitar um pouco a vida, vamos usar coordenadas esféricas deslocadas, ok?
Assim, o centro das coordenadas é o centro da esfera, isso vai nos ajudar bastante.
Passo 4
Precisamos escrever matematicamente a região de integração. Como nós deslocamos as coordenadas para o centro da esfera, ela passa a ser escrita como , no caso:
Você pode verificar isso fazendo a mudança esférica na sua equação!
O termo da equação vai ser cancelado pelo da mudança esférica.
Bom, como se trata da esfera inteira, , o que nos dá:
Passo 5
Opa, mas ta faltando uma coisa né? Só queremos a parte ! O que podemos fazer então é achar o valor da integral na parte onde e aí diminuir um do outro! (sim, isso é mais fácil do que achar direto o valor da parte , acredite haha).
Vamos começar achando os limites do nosso raio! Para isso vamos igualar a zero:
Como queremos pegar toda a área abaixo de , esse é nosso limite inferior e ficamos com:
Aí você pode pensar, “ué, então o pode ser negativo? Se ele é o raio não consideramos só valores positivos?” Pois ai eu te falo que vai ser positivo!
Vamos dar uma olhada nos limites de pra perceber isso! O limite superior dele vai ser o de sempre. E o inferior vai ser onde o plano corta a esfera:
Logo,
E nesse intervalo de , ! Por isso o vai ser sempre positivo ;)
E claro, o vai ir de a mesmo. Então ficamos com:
Passo 6
Vamos temos fazer a substituição esférica na integral:
Passo 7
Vamos resolver primeiro a integral em . Integrando em relação a :
Passo 8
Agora em relação a :
Passo 9
Agora vamos integrar em relação a :
Passo 10
Agora é a vez da integral em . Integrando em :
Integrando em :
Quebrando isso aí pra facilitar:
A última! Calma que ta acabando!
Juntando tudo:
Passo 11
Só lembrando caso você tenha esquecido (porque essa questão foi enorme), nosso objetivo aqui é calcular a massa daquela porção de esfera. Agora finalmente temos todas as informações que precisamos: