Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Centro de Massa e Centroide de Sólidos

Ver Teoria
Exercício 7123456891011121314151617181920

Enunciado

Coordenadas cilíndricas

Seja R a região interior à esfera x 2 + y 2 + z 2 = 9 que satisfaz x 2 + y 2 - z 2 ≤ 1 e z ≥ 0 .

  1. Descreva R em coordenadas cilíndricas.
  2. Supondo que a densidade é δ x , y , z = z , determine a massa R .

Passo 1

Letra a)

Vamos fazer um esboço da região W para entender melhor o que está sendo pedido

A equação x 2 + y 2 + z 2 = 9 representa uma esfera de raio 3 . A outra equação x 2 + y 2 - z 2 = 1 representa um hiperboloide de uma folha. Se você reparar, a equação é bem parecida com a do cone, a diferença é que temos um número independente (no caso, o 1 ), não apenas as variáveis. Realmente, o hiperbolóide tem certa semelhança com o cone, não é? Olha só:

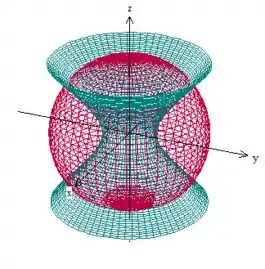
O problema diz que R é a região dentro da esfera e do paraboloide, com z > 0 , portanto:

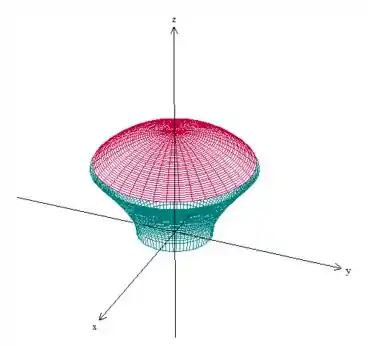
Passo 2

Agora precisamos escrever essa região W em coordenadas cilíndricas, como o problema pede. Faremos:

x = r cos ⁡ θ

y = r   s e n   θ

z = z

J = r

Vamos agora fazer essa substituição na equação do hiperboloide e na da esfera:

x 2 + y 2 = 1 + z 2   → r cos ⁡ θ 2 + r   s e n   θ 2 = 1 + z 2    

r 2 = 1 + z 2

x 2 + y 2 + z 2 = 9   → r cos ⁡ θ 2 + r   s e n   θ 2 + z 2 = 9

r 2 = 9 - z 2

Pela figura, vemos que, na parte de baixo do sólido, r varia desde o eixo z até a superfície do paraboloie e na parte de cima, desde o eixo z até a superfície da esfera. Prontanto, nós teremos que dividir nossa região em duas partes para descrevê-la em coordenadas cilíndricas (se você seguir o mesmo raciocínio para a coordenada z , chegará à mesma conclusão).

Vamos chamar esse “tronco” formado pelo paraboloide de R 1 e a “tampa” formada pela esfera de R 2 , temos R = R 1 + R 2 .

Para R 1

Temos o raio entre 0 e o paraboloide, logo, 0 ≤ r ≤ z 2 + 1 .

Vemos, também, que 0 ≤ θ ≤ 2 π , uma vez que o sólido está envolta do eixo de simetria z . Já a coordenada z varia desde z = 0 até o ponto em que as superfícies se encontram.. Para isso, temos que encontrar a altura onde as superfícies se cortam:

r 2 = 1 + z 2 = 9 - z 2

2 z 2 = 8

z = 2

Assim, escrevermos a região como:

R 1 = { ( r , θ , z ) | 0 ≤ r ≤ 1 + z 2 ; 0 ≤ θ ≤ 2 π ;   0 ≤ z ≤ 2 }

Para R 2

Temos o raio variando entre 0 e a superfície da esfera, logo, 0 ≤ r ≤ 9 - z 2 . Novamente, 0 ≤ θ ≤ 2 π . E z vai desde a interseção entre as superfícies, z = 2 até o topo da esfera z = 3 (é o raio da esfera).

Temos então:

R 2 = { ( r , θ , z ) | 0 ≤ r ≤ 9 - z 2 ; 0 ≤ θ ≤ 2 π ;   2 ≤ z ≤ 3 }

Passo 3

Letra b)

O problema pede que calculemos a massa do sólido delimitado pelas superfícies acima, sabendo que sua densidade é dada por δ x , y , z . Nós sabemos que:

d m =   δ x , y , z d V

Onde d m é o diferencial de massa e d V o de volume. Integrando ambos os lados na região R em que o sólido está contido, temos que:

M = ∭ R   δ x , y , z d V

M = ∭ R 1   z   d x d y d z + ∭ R 2   z   d x d y d z

Passo 4

Vamos agora substituir os intervalos que encontramos nas integrais:

= ∫ 0 2 π ∫ 0 2 ∫ 0 1 + z 2 z   r d r d z d θ + ∫ 0 2 π ∫ 2 3 ∫ 0 9 - z 2 z   r d r d z d θ =

Passo 5

Agora vamos integrar em relação a r :

= ∫ 0 2 π ∫ 0 2 z r 2 2 0 1 + z 2 d z d θ + ∫ 0 2 π ∫ 2 3 z r 2 2 0 9 - z 2 d z d θ =

= 1 2 ∫ 0 2 π ∫ 0 2 z ( 1 + z 2 ) d z d θ + 1 2 ∫ 0 2 π ∫ 2 3 z ( 9 - z 2 ) d z d θ =

= 1 2 ∫ 0 2 π ∫ 0 2 z + z 3 d z d θ + 1 2 ∫ 0 2 π ∫ 2 3 9 z - z 3 d z d θ =

Passo 6

Agora em relação a z :

= 1 2 ∫ 0 2 π z 2 2 + z 4 4 0 2 d θ + 1 2 ∫ 0 2 π ∫ 2 3 9 z 2 2 - z 4 4 2 3 d θ =

= 1 2 ∫ 0 2 π 2 + 4 d θ + 1 2 ∫ 0 2 π 81 2 - 81 4 - 18 + 4 d θ =

= 3 ∫ 0 2 π d θ + 25 8 ∫ 0 2 π d θ =

Passo 7

Finalmente, em relação a θ :

= 6 π + 25 π 4 =

= 49 π 4

Resposta

49 π 4

Exercícios de Livros Relacionados

Determine a massa e o centro de massa do sólido dado E com função densidade dada ρ . E é o tetraedro limitado pelos planos x = 0 ,y = 0 ,z = 0 ,x + y + z = 1 ρ x , y , z = y
Utilize coordenadas esféricas.Determine o centroide do sólido do exercício 25.
Determine o centro de massa de uma semi-esfera, cuja densidade no ponto P é proporcional à distância de P ao centro.
Estabeleça, mas não calcule, as expressões integrais para (a) a massa, (b) o centro de massa e (c) o momento de inercia em relação ao eixo z.39. O sólido do exercício 19; ρ x , y , z = x 2 + y 2
Estabeleça, mas não calcule, as expressões integrais para (a) a massa, (b) o centro de massa e (c) o momento de inercia em relação ao eixo z.40. O hemisfério x 2 + y 2 + z 2 ≤ 1 , z ≥ 0 ;ρ x , y , z =