Tipler, Mosca; Física Para Cientistas e Engenheiros; 6ª Ed. - Capítulo 10, Seção 1, Questão 68.
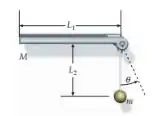
(Cap 10 – Ex 68) Uma barra uniforme, de comprimento igual a e massa igual a , está presa a uma dobradiça de massa desprezível em uma das extremidades e é livre para girar no plano vertical (Figura 10-55). A barra é largada do repouso na posição mostrada. Uma partícula, de massa , está suspensa da dobradiça por um fio fino de comprimento igual a . A partícula gruda da barra quando as duas encostam e após a colisão, a barra continua a gira até . (a) Determine . (b) Quanta energia é dissipada na colisão?
Passo 1
a) Oi pessoal, tudo bem? Vamos analisar essa questão.
Como o torque externo que atua no sistema é zero, a quantidade de movimento angular é conservada nessa colisão perfeitamente inelástica e a energia mecânica também.
A ideia é a gente usar as expressões da conversação para achar a massa da partícula, como ele pede.
Vamos começar fazendo a conservação de energia somente da barra entre dois momentos em que ela não chega a encostar na partícula, por isso a partícula não vai influenciar essa conservação.
O momento inicial é o momento onde ela está parada, então , porque a velocidade é nula. O momento final vai ser o momento onde a barra está quase na vertical quase tocando a partícula, mas ela ainda não se tocaram.
A energia cinética final da barra, que só está girando, é dada por
Vamos colocar o referencial de altura a uma distância abaixo da barra. Assim a energia potencial é em relação ao seu centro, que fica na altura no começo e na altura no final. Então temos:
Subsituindo tudo na conservação de energia
Logo:
Passo 2
Vamos agora chamar de , a velocidade angular do conjunto logo após o impacto. Usando a conservação de momento angular temos
Onde o momento inicial é quando a barra está quase encostando na partícula, mas ainda não encostou. Então o momento é só o momento da barra. Vamos usar a fórmulinha
O momento de inércia em relação a extremidade (que é onde está nosso eixo de rotação aqui) de uma barra é
Assim
O momento final é dado pela barra e a partícula se movendo juntas com uma velocidade angular só.
Esse momento de inércia vai ser a soma dos momentos da partícula e da barra. Já sabemos o da barrra. E o da partícula é dado por
Assim
Usando conservação de quantidade de movimento angular, temos:
Logo:
Substituindo os dados , e
Passo 3
Falta achar , né? Vamos aplicar a conservação de energia novamente. Mas agora, o momento inicial vai ser quando a partícula e barra começam a se mover juntas e o final vai ser quando elas estão no ângulo máximo de . Temos:
Para o momento inicial, a energia cinética é
O momento final não tem energia cinética porque a barra está na altura máxima, o que implica velocidade nula. E a pontencial é a soma das energias da partícula e da barra.
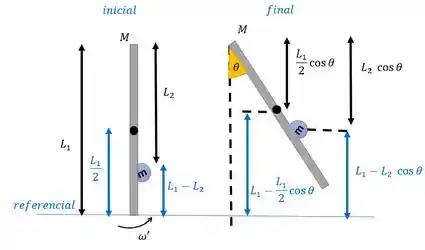
A da partícula é
E da barra é
Substituindo na expressão da conservação de energia:
Abrindo e rearrumando:
Passo 4
Sabemos que o momento de inércia do conjunto é
Substituindo na equação da energia
Substituindo nossos dados
Resolvendo:
Passo 5
Item (b):
A energia dissipada na colisão inelástica é dada pela diferença entre a energia no início de tudo quando tá todo mundo parado e no final quando o conjunto está na altura máxima. Vimos que para os dois casos , porque não há velocidade. Então a variação de energia é dada por
A energia inicial é quando tá todo mundo parado. A da barra é
E a da partícula
Assim
Substituindo os valores:
Passo 6
E a final é a energia potencial total
Substituindo os dados:
Portanto: