Calcule as derivadas laterais de no ponto .
Passo 1
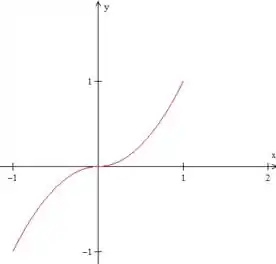
Repara, a função é contínua em , como vemos no gráfico. Portanto, para achar as derivadas laterais dessa função nesse ponto basta derivá-las de primeira, pelo método da teoria.
Passo 2
A derivada pela esquerda, em relação ao ponto , vai ter como fórmula o seguinte:
Como :
Passo 3
A derivada pela direita, em relação ao ponto , vai ter como fórmula o seguinte:
Como :
Resposta
Exercícios de Livros Relacionados
Nos exercícios 1 a 5 calcular as derivadas laterais nos pontos onde a função não é derivável. Esboçar gráfico. f x = 2 | x - 3 |
Seja f x = x 2 - 1 ,s ex ≤ 1 1 - x 2 ,s ex1 Esboçar o gráfico de f ;Verificar se f é contínua nos pontos - 1 e 1 ;Calcular f ' - 1 - ,f ' - 1 + ,f ' 1 -ef ' ( 1 + ) ;Calcular f ' ( x ) , obter o seu d
Encontrar as derivadas laterais das seguintes funções, nos pontos indicados. Encontrar os intervalos onde f ' x0 e f ' x0 .
Nos exercícios 1 a 5 calcular as derivadas laterais nos pontos onde a função não é derivável. Esboçar gráfico. f x = 2 - x 2 ,x- 2 - 2 , x ≤ 2 2 x - 6 ,x2
Nos exercícios 1 a 5 calcular as derivadas laterais nos pontos onde a função não é derivável. Esboçar gráfico. f x = 1 - x 2 ,x1 0 , x ≤ 1