Considere os seguintes pontos no espaço tridimensional:
(a) Encontre um vértice de modo que os pontos e formem um paralelogramo.
(b) Encontre a área do paralelogramo obtido acima.
(c) Encontre a equação do plano que passa pelos pontos . Verifique se o ponto pertence a esse plano.
Passo 1
(a) Oláaa! Como a gente está no espaço 3D, é mais difícil de desenhar as coisas e visualizar o que está acontecendo, vou te dar uma regrinha de como achar esse ponto que ele falou, tá? Vai ser um bizu para facilitar nossa vida.
Se a gente tem 3 pontos e no espaço, para achar um ponto que forme um paralelogramo com eles, a gente pode começar calculando dois vetores que saiem de um de seus vértices, por exemplo, o . Calculamos e :
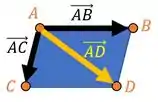
Repara aí uma coisa nesse desenho. Se a gente lembrar de soma vetorial, vemos graficamente que:
Como a gente consegue achar e , e já temos , conseguimos achar por essa relação aí a coordenada de ! Vem comigo!
Passo 2
Para escrever esses 3 vetores, é só fazer a coordenada do ponto final menos a coordenada do ponto inicial. Aí podemos escrever:
Substituindo ali na soma entre vetores:
Prontinho!
Passo 3
(b) Podemos calcular a área desse paralelogramo a partir dos vetores e que a gente achou. Nossa figura é descrita por eles, olha lá:
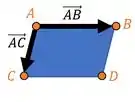
Aí para calcular a área desse paralelogramo calculamos o módulo do produto vetorial entre esses vetores. Assim:
Vamos calcular o produto vetorial:
Aí a área fica:
Passo 4
(c) Para achar a equação do plano que passa por esses pontos, a gente precisa usar a fórmulinha:
Onde é um vetor normal ao nosso plano. Repara que a gente calculou ele. Por que? Nossos vetores estavam na direção de dois lados de nosso paralelogramo. Isso quer dizer que eles estão dentro do plano formado pelos nossos pontos.
Ou seja, a gente tinha dois vetores paralelos ao plano e calculou o produto vetorial entre eles. Isso nos dá um vetor normal a esses dois vetores, e logo, um vetor normal ao plano.
E é um ponto que pertence ao plano. Podemos escolher qualquer um dos nossos 3 pontos. Aí podemos escrever:
Nossa fórmulinha fica:
Passo 5
Agora é ver se o ponto pertence a esse plano. Como? Para um ponto pertencer a um plano, as coordenadas dele devem satisfazer a equação do plano.
Então tudo que a gente precisa fazer é substituir na equação
Fica assim:
Como esse ponto satisfaz nossa equação, pertence ao nosso plano .
É isso! Arrasamos!
Resposta
(a)
(b)
(c)
pertence ao plano