Uma banqueta de três pernas está submetida à carga , como mostrado. Determine a força de reação vertical sob cada perna. Despreze o peso da banqueta.
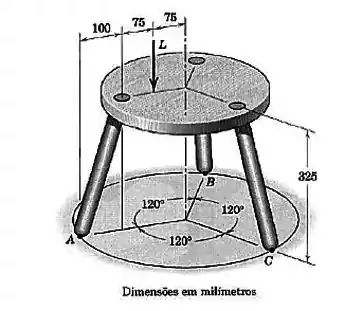
Passo 1
O que queremos saber nessa questão é quais são os módulos das forças de reação: e.
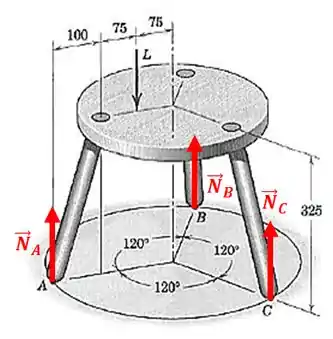
Em primeiro lugar, veja que as forças de reação em e serão iguais. Por quê? Porque existe um plano de simetria passando entre e
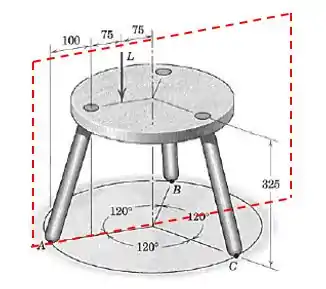
Esse plano divide a figura em duas partes iguais. Faz sentido pensar que tudo que ocorrer fisicamente em uma metade ocorrerá na outra também, não é mesmo?
Passo 2
Agora vamos testar o equilíbrio de momentos em relação ao eixo
Mas vamos ser espertos: passaremos o eixo em cima do ponto Dessa forma, o momento que realizar será nulo em relação a esse eixo:
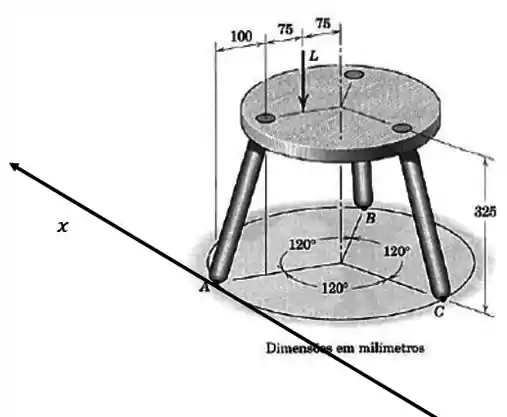
Passo 3
Beleza! Agora só precisou calcular o momento que cada força faz em relação a esse eixo.
Assim de cara, perceba que as forças de reação apontarão na direção contrária à força .
Além disso, veja que a direção horizontal da força até o eixo é de:
.
Assim, podemos dizer que o momento da força é dado por:
Vamos atribuir a este momento o valor positivo. E o valor negativo ao momento das outras forças.
Passo 4
Bom, vamos às outras forças. Em primeiro lugar, pela simetria, como vimos, elas serão iguais:
E qual será a distância das forças até o eixo?
Temos que usar um pouco de trigonometria:
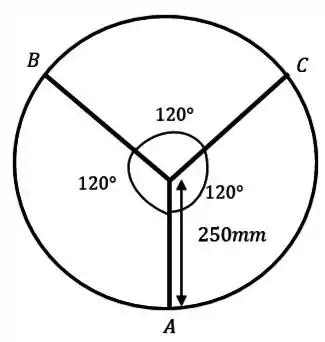
Essa é a vista de cima da projeção do banco no chão.
Qual é a distância de até
Basta a gente formar o triângulo abaixo em cima da figura:
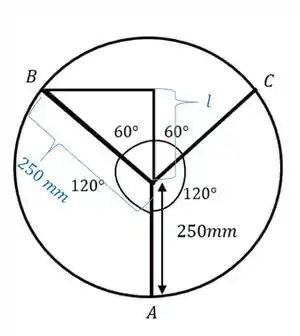
Em outras palavras, a distância vai ser igual a mais o lado () do triângulo acima. Podemos calcular o lado usando trigonometria:
Então, a distância total do ponto até o ponto é:
E a distância de até Mesma coisa, já que é simétrico:
Passo 5
Beleza, então os momentos de cada força valerão:
Usando a relação:
Simplificando e isolando essa parada:
Passo 6
Beleza, mas falta achar . Agora ficou fácil: Bata a gente usar o equilíbrio das forças:
Perceba que a forças normais apontam em um sentido contrário ao da força Assim: