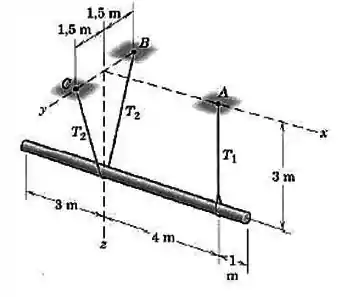
O eixo horizontal de aço tem uma massa de e está suspenso por um cabo vertical em e por um segundo cabo que passa por baixo do eixo e está situada em um plano vertical transversal. Calcule as forças trativas e nos cabos.
Passo 1
Para que o sistema esteja em equilíbrio, as duas condições abaixo precisam ser satisfeitas:
A configuração das forças é mais ou menos assim:
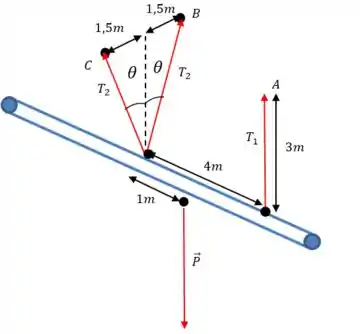
Pela figura do enunciado dá para notar que a barra tem de comprimento. Sendo assim, o peso é aplicado no centro da barra, numa distância de de cada extremidade.
Ainda pela figura do enunciado, vemos que as forças de valor são aplicadas a uma distância de da extremidade. Sendo assim, o peso será aplicado a uma distância de do ponto de aplicação das forças.
Passo 2
Vamos calcular os momentos das forças em relação ao eixo que passa em .
Nesse caso, perceba que as duas forças de valor não exercem momento em relação a esse eixo.
Só o peso e a exercem.
Vamos calcular o módulo do peso da barra:
Perceba que essas forças geram momentos de sentidos contrários. Assim:
Passo 3
Agora ficou mais fácil, vamos usar a segunda condição para achar .
Antes disso, veja que a gente tem que pegar apenas a componente vertical da força ():
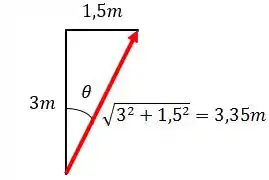
Ou seja:
Passo 4
Bom, mas são duas forças, então:
Observando o nosso triângulo, vemos que o cosseno do ângulo é:
Substituindo isso na equação de , temos que:
Assim: