Uma área retangular deve ser dividida ao meio, como indica a figura. Se você puder dispor de m de cerca, qual é a área máxima que consegue delimitar?

Passo 1
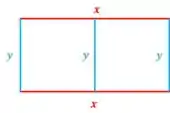
Vamos considerar a altura como e o comprimento como . Beleza. O perímetro será:
Pegando os três pedações verticais () e os dois horizontais () da figura.
Passo 2
A área do retângulo, por sua vez, será sempre base vezes altura, ou seja:
A partir da primeira equação, podemos substituir um dos valores. Isolando o :
Substituindo agora na equação da área:
Oh não! É uma parábola!!!!
Passo 3
Lembra que a gente está buscando área máxima que conseguimos delimitar? Então dentro da nossa função, a gente vai ter que buscar o máximo da parábola. E onde ela fica? No ponto de vértice:
Sabe o que aconteceu em ? Os Aliados invadiram a Normandia como parte da Operação (Dia D) para libertar a França dos Alemães. O que isso tem a ver com a questão? Nada!