Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei da Refração

Ver Teoria
Exercício 712345689101112131415161718192021222324252627282930

Enunciado

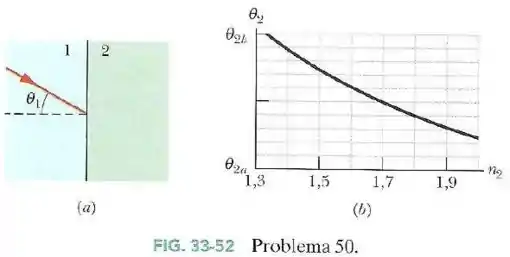
Na Fig.33-52a um feixe luminoso que está se propagando inicialmente no material 1 incide no material 2 com um ângulo de 30 ° . A refração da luz no material 2 depende, entre outros fatores, do índice de refração n 2 do material 2 .

A Fig.33-52b mostra o ângulo de refração θ 2 em função de n 2 . A escala do eixo vertical é definida por θ 2 a = 20,0 ° e θ 2 b = 40,0 ° .

  1. Qual é o índice de refração do material 1 ?
  2. Se o ângulo de incidência aumenta para 60 ° e n 2 = 2,4 , qual é o valor de θ 2 ?

Passo 1

Letra a)

A dependência do ângulo de refração com o índice de refração do meio 2 é dada pela Lei de Snell:

n 1 sen ⁡ θ 1 = n 2 sen ⁡ θ 2

Nós temos o ângulo de incidência θ 1 = 30 ° . Agora, precisamos de algum ponto no gráfico que nos dê θ 2 e n 2 , para podermos substituir e achar n 1 .

Um ponto no gráfico que vai facilitar o nosso trabalho é o correspondente a n 2 = 1,7 , pois para este ponto o ângulo dado pela escala do eixo vertical é θ 2 = 30 ° .

(no eixo vertical, os limites são 20,0 ° e 40,0 ° , e o nosso ponto é exatamente o ponto médio, logo 30,0 ° ).

Ficamos com:

n 1 sen ⁡ 30 ° = 1,7 ∙ sen ⁡ 30 °

n 1 = 1,7

Passo 2

Letra b)

Graças ao gráfico, nós já temos o índice de refração n 1 . Com posse dos valores de θ 1 = 60 ° e n 2 = 2,4 , podemos substituí-los na Lei de Snell:

n 1 sen ⁡ θ 1 = n 2 sen ⁡ θ 2

1,7 ∙ sen ⁡ 60 ° = 2,4 ∙ sen ⁡ θ 2

sen ⁡ θ 2 = 1,7 ∙ 3 2 2,4 ≅ 0,613

θ 2 ≅ sen - 1 ⁡ 0,613 ≅ 37,84 °

Resposta

Letra a)

n 1 = 1,7

Letra b)

θ 2 ≅ 37,84 °

Exercícios de Livros Relacionados

Uma esfera transparente de índice de refração n , espelhada numa calota A B da sua superfície, com centro em C (fig.), é usada como retro-refletor: qualquer raio 1 paralelo ao eixo C D e paraxial (pró
O índice de refração de um meio inomogêneo, em função da altitude z , é dado por n = n 0 + n ' z , onde n 0 e n ' são constantes. Um raio luminoso no plano ( x z ) parte da origem numa direção de cose
Um raio de luz no ar incide na superfície de um pedaço de vidro. O ângulo entre a normal à superficie e o raio incidente é 40°, e o ângulo entre a normal e o raio refratado é 28°. Qual é o ângulo entr
• O material A tem um índice de refração maior que o material B. Qual material tem um ångulo crítico maior para a reflexão interna total quando estiver no ar? (a) A, (b) B, (c) os angulos são iguais.