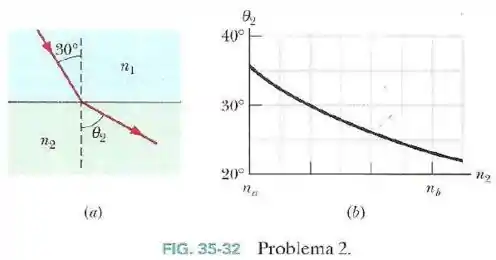
Na Fig.35-32a, um raio luminoso que estava se propagando no material incide em uma interface com um ângulo de . O desvio sofrido pelo raio devido à refração depende, em parte, do índice de refração do material .
A Fig.35-32b mostra o ângulo de refração em função de . A escala do eixo horizontal é definida por e .
Qual é a velocidade da luz no material ?
Passo 1
Para sabermos a velocidade da luz no material precisamos primeiro conhecer o índice de refração . Vamos usar o gráfico para encontra-lo.
A dependência do ângulo de refração com o índice de refração é dada pela lei de Snell:
Sabemos o ângulo de incidência . O ponto no gráfico correspondente a vai ser aquele onde .
Passo 2
Pela escala do eixo horizontal, cada unidade (traço mais escuro) é dada por:
(pois entre e temos três unidades)
Sendo o ângulo de corresponde à uma unidade depois de , temos que .
Pelo que falamos antes, teremos;
Passo 3
O índice de refração de um material é definido como:
Onde é a velocidade da luz no material, é a velocidade da luz no vácuo e é o índice de refração do material .