Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Elípticas

Ver Teoria
Exercício 101234567891112131415

Enunciado

  1. Calcule as seguintes integrais:

d )     ∬ D sin ⁡ 4 x 2 + y 2   d x d y ,

D = x ,   y ; 4 x 2 + y 2 ≤ 1 ,   y ≥ 0

Passo 1

Bem, a primeira coisa que iremos fazer aqui é entender quem é essa região que estamos trabalhando.

Primeiramente, a região D é formada pela inequação 4 x 2 + y 2 ≤ 1 . Mas... Se ao invés de pegarmos a inequação, olhássemos para a equação

4 x 2 + y 2 = 1

RARA! Essa equação nos representa uma... elipse centrada na origem:

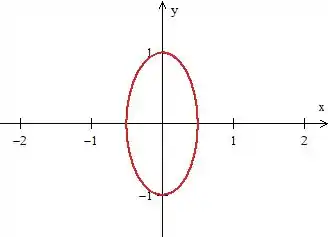
A inequação indica que estamos dentro dela...

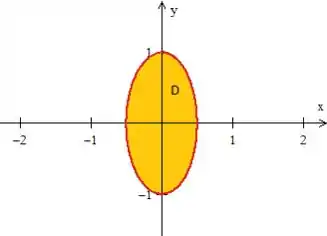
Mas calma! A região D também foi delimitada por y ≥ 0 , o que significa que estamos trabalhando apenas a parte de cima. Veja!

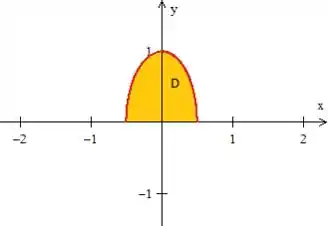
Passo 2

Então! Estamos trabalhando com uma superfície elíptica e, além disso... A equação que está dentro do seno também é bem peculiar o que nos sugere uma... Mudança para coordenadas elípticas !

Podemos, então, pensar na comparação com a equação fundamental da trigonometria

4 x 2 + y 2 = 1     →           2 x 2 + y 2 = 1

                                                                    cos 2 ⁡ θ + sin 2 ⁡ θ = 1

onde podemos falar que

x = 1 2 r cos ⁡ θ

e

y = r sin ⁡ θ

O Jacobiano desse tipo de mudança é o produto dos números que estão atrás desses caras pelo r ...

J = 1 2 ∙ 1 ∙ r

sacou?

Passo 3

Se lembre também que não podemos terminar uma mudança sem antes sabermos onde estão variando os novos caras, no caso, r e θ :

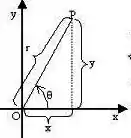
Por comparação com...

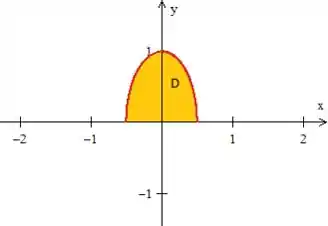
podemos ver que θ dá uma meia volta

0 ≤ θ ≤ π

enquanto que o r varia da origem até a curva vermelha

0 ≤ r ≤ c u r v a   v e r m e l h a

como a curva vermelha é

4 x 2 + y 2 = 1

substituindo as coordenadas...

4 1 2 r cos ⁡ θ 2 + r sin ⁡ θ 2 = 1

e simplificando um pouco encontramos...

4 ∙ 1 4 r 2 cos 2 ⁡ θ + r 2 sin 2 ⁡ θ = 1

r 2 cos 2 ⁡ θ + sin 2 ⁡ θ = 1

r = 1

que r máximo é 1

0 ≤ r ≤ c u r v a   v e r m e l h a

0 ≤ r ≤ 1

Passo 4

Finalmente, regressando à integral que queremos resolver

∬ D sin ⁡ 4 x 2 + y 2   d x d y =

vamos simplesmente substituir tuuuudo o que encontramos nos passos anteriores!

∬ D r θ sin ⁡ 4 1 2 r cos ⁡ θ 2 + r sin ⁡ θ 2   J d r d θ

Duas observações com relação a essa mudança que fizemos:

  1. Você pode notar que trocamos D por D r θ , afinal antes trabalhávamos com um domínio em x e y e agora mudou para r e θ (é apenas uma questão de notação, mas é importante )
  2. Multiplicamos pelo Jacobiano (nunca se esqueça)

Mas enfim! Podemos continuar a integral simplificando aqueles termos dos parênteses...

∬ D r θ sin ⁡ 4 1 4 r 2 cos 2 ⁡ θ + r 2 sin 2 ⁡ θ   J d r d θ =

Simplificando tuuuudo:

∬ D r θ sin ⁡ r 2 cos 2 ⁡ θ + r 2 sin 2 ⁡ θ   J d r d θ =

∬ D r θ sin ⁡ r 2 cos 2 ⁡ θ + sin 2 ⁡ θ   J d r d θ =

∬ D r θ sin ⁡ r 2   J d r d θ

Podemos trocar esse jacobiano e também esse D r θ ...

∬ D r θ sin ⁡ r 2   J d r d θ = ∫ 0 π ∫ 0 1 sin ⁡ r 2 1 2 r   d r d θ

agora é só resolver essa integral aí! BOOORA?

Passo 5

Vamos começar resolvendo essa integral aí como nos manda o figurino e fazendo a integral de dentro primeiro

1 2 ∫ 0 π ∫ 0 1 sin ⁡ r 2 r   d r d θ

essa integral de dentro se resolve fácil fazendo a substituição simples...

r 2 = u

d u = 2 r d r                   →                           r d r = d u 2

Não se esqueça de trocar também os limites, heim!

r = 0                 →                   u = r 2                   →                         u = 0 2 = 0

r = 1                 →                   u = r 2                   →                         u = 1 2 = 1

Nesse caso não mudou muito não . Mas enfim! Substituindo...

1 2 ∫ 0 π ∫ 0 1 sin ⁡ u d u 2 d θ =

1 4 ∫ 0 π ∫ 0 1 sin ⁡ u d u d θ =

e calculando

1 4 ∫ 0 π - cos ⁡ θ 0 1 d θ =

1 4 ∫ 0 π - cos ⁡ 1 - - cos ⁡ 0 d θ =

1 4 1 - cos ⁡ 1 ∫ 0 π d θ =

obteremos...

π 4 1 - cos ⁡ 1

Resposta

π 4 1 - cos ⁡ 1

Exercícios de Livros Relacionados

Seja σ θ ,ρ = 2 ρ cos ⁡ θ ,ρ s e nθ . Mostre que σ transforma a reta ρ = 1 numa elipse. Desenhe tal elipse.
Calcule a área da região delimitada pela elipse
Seja σ a transformação do Exercício 10. Desenhe σ ( B ) onde B é o retângulo 0 ≤ ρ ≤ 1 , 0 ≤ θ ≤ 2 π .