Exercícios de Mudança para Coordenadas Elípticas - Lista de Exercícios Resolvida

Sabendo que é a região em que e que , calcule a seguinte integral dupla

Encontre o valor da área do domínio plano situado no primeiro quadrante acima de e limitado por, .

Calcule , onde é a região limitada pela elipse de equação .

Calcule a área da figura plana limitada pela curva dada pela equação .

Seja o domínio do dado por . Calcule

Sugestão: Faça , e escolha a constante de forma que o termo misto desapareça do integrando.

Mostre, usando integral dupla, que a área limitada pela elipse é igual a .

Determine a área delimitada no plano () pela elipse

Calcule a integral dupla

Onde

Encontre o valor da área do domínio plano situado no primeiro quadrante e limitado por , , .

1. Calcule as seguintes integrais:

Seja o domínio do dado por . Calcule

Sugestão: Faça , e escolha a constante de forma que o termo misto desapareça do integrando.

Questão 1: Calcule a área da região plana

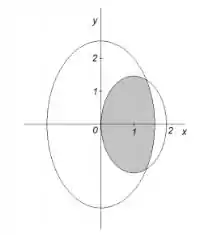
(Dica: Fazer uma mudança de variáveis compatível com a equação da maior elipse).

Calcule a área da região do plano limitada pela elipse .

Seja uma unção contínua arbitrária em e . É correto concluir que no caso em que

Calcule a integral usando a transformação

Onde é a região limitada pela elipse